§ 1. Погрешность

Погрешность моделей и методов

Решение прикладных задач можно разбить на три этапа: математическая модель, численные метод и программная реализация. На каждом этапе исследователю приходится иметь дело с разного рода погрешностями:

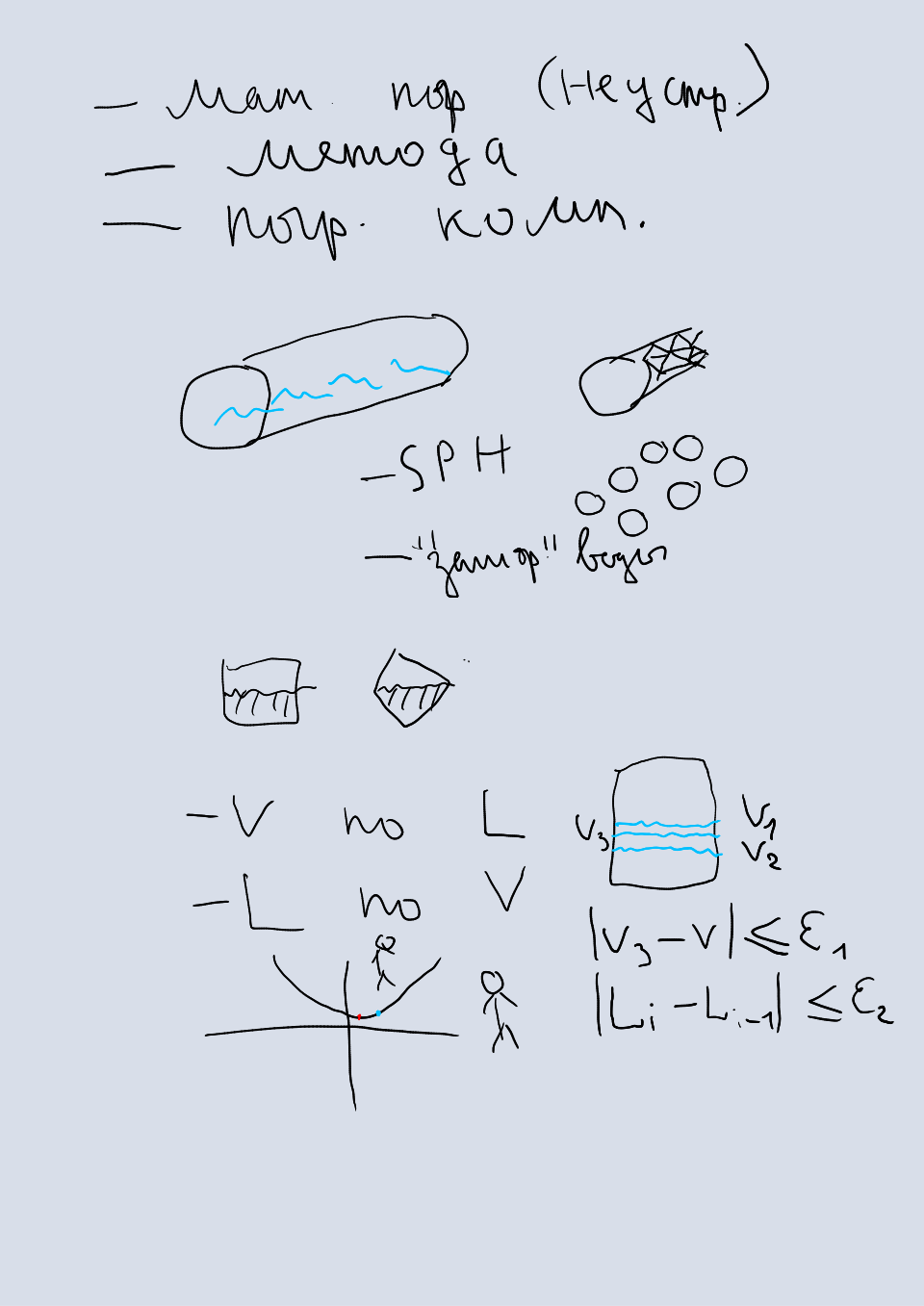
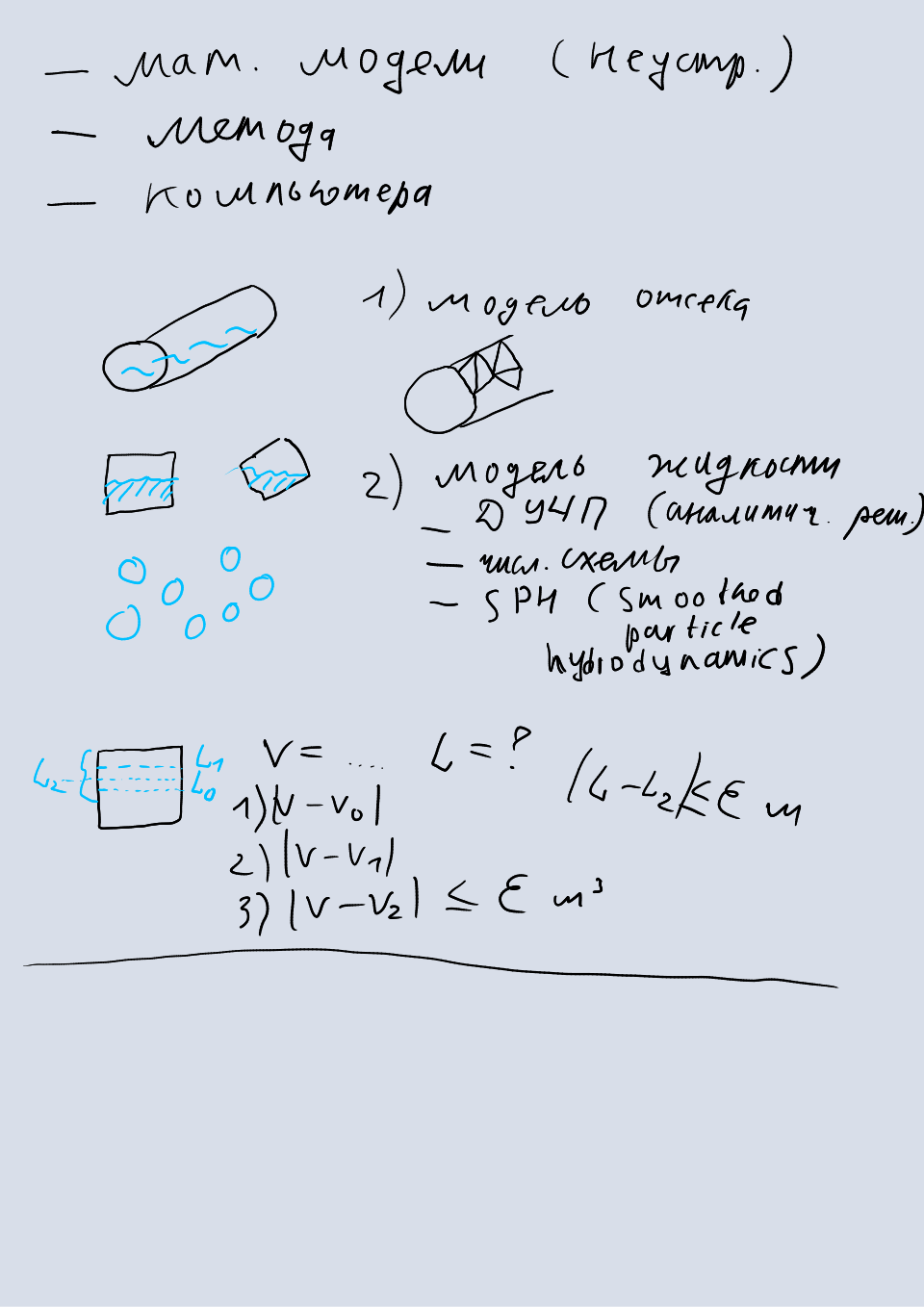
• погрешностью математической модели,
• погрешностью численного метода,
• погрешностью компьютера.

Чтобы разобраться этих разновидностях погрешности, удобно рассмотреть их на реальной задаче. Для этого возьмем задачу затопления отсеков морского объекта жидкостью. Под морским объектом понимается все, что плавает: суда, корабли, подводные лодки, плавучие нефтедобывающие платформы и др. В качестве входных данных мы имеем геометрию отсека и объем жидкости, которая попала в отсек. В качестве выходных данных мы имеем уровень жидкости в отсеке (или распределение частиц жидкости по отсеку в наиболее общем случае), по которому легко вычислить центр масс жидкости в отсеке, который и представляет интерес в реальных приложениях.

В данной задаче используются две математических модели: геометрическая модель отсека и модель движения жидкости. В качестве модели отсека может использоваться либо геометрическая фигура (цилиндр, параллелепипед и др.), которая точно описывает геометрию отсека, либо многогранник (множество вершин, соединенных треугольными гранями), который дает приближенное описание геометрии отсека. В большинстве случаев используют приближенное описание, потому что оно наиболее общее и распространено в трехмерной графике. Однако, такое описание вносит в вычисления погрешность, которая называется погрешностью математической модели. Иногда такую погрешность называют неустранимой, поскольку на нее можно повлиять, только путем изменения модели. В качестве модели движения жидкости может использоваться либо так называемая модель замороженной воды, в которой жидкость движется без образования волн (то есть поверхность всегда идеально гладкая), либо более сложная модель сглаженных частиц, в которой жидкость движется по законам, приближенным к реальным.

В задаче затопления отсеков используется численный метод для определения уровня жидкости в отсеке по известному объему. В качестве такого метода можно использовать любой метод оптимизации (то есть метод, который ищет экстремум целевой функции): например, метод бисекции. В качестве целевой функции используется разность заданного объема жидкости и объема жидкости при известном уровне, а метод подбирает уровень, при котором эта разность близка к нулю. Погрешность метода оптимизации настраивается с помощью параметров: количество итераций, погрешность аргумента, погрешность функции. Возможность задания целевых значений погрешности метода является главным ее отличием от погрешности математической модели, которую задать невозможно. Также эта погрешность не может быть меньше компьютерной.

Наконец, поскольку мы решаем данную задачу на компьютере, в ней присутствует погрешность вычислений этого компьютера. Числа в компьютере кодируются ограниченным количеством разрядов, и в случае вещественных чисел это означает, что в промежутке между нулем и единицей располагается конечное множество вещественных чисел. Ограниченное количество разрядов и является причиной возникновения погрешности компьютера, которую мы рассмотрим более подробно в следующем разделе.

Погрешность компьютера

Вещественные числа в памяти компьютера кодируются последовательностью разрядов (бит), в которой есть три компоненты: знак, экспонента и мантисса. Число типа float восстанавливается из этих трех копонент по формуле $(-1)^S \, 2^{E-127} \left( 1 + \sum\limits_{i=1}^{23}M_{23-i}2^{-i}\right)$, где S — знак, E — экспонента, восстановленная из разрядов как целое беззнаковое число по формуле $E = \sum\limits_{i=0}^{7} E_i 2^{i}$ , M — мантисса, которая используется в формуле поразрядно. Аналогичная формула используется для чисел типа double: $(-1)^S \, 2^{E-1023} \left( 1 + \sum\limits_{i=1}^{52}M_{52-i}2^{-i}\right)$, где $E = \sum\limits_{i=0}^{10} E_i 2^{i}$.

Для того чтобы разобраться, как это кодирование влияет на погрешность, расммотрим числа, которые не имеют точного представления в памяти компьютера. Для этого напишем программу на C++, которая выводит двоичное представление числа в памяти:

#include <iostream>
#include <bitset>

void print(float f) {
    std::cout << std::bitset<32>(*reinterpret_cast<uint32_t*>(&f)) << '\n';
}

int main() {
    print(0.f + 1.f/3.f);
    print(1.f + 1.f/3.f);
    print(2.f + 1.f/3.f);
    print(3.f + 1.f/3.f);
    print(4.f + 1.f/3.f);
    print(5.f + 1.f/3.f);
    print(6.f + 1.f/3.f);
    print(7.f + 1.f/3.f);
    print(8.f + 1.f/3.f);
}

Эта программа выводит следующее (пробелы добавлены для читаемости):

0 01111101 01010101010101010101011
0 01111111 01010101010101010101011
0 10000000 00101010101010101010101
0 10000000 10101010101010101010101
0 10000001 00010101010101010101011
0 10000001 01010101010101010101011
0 10000001 10010101010101010101011
0 10000001 11010101010101010101011
0 10000010 00001010101010101010101

В выводе программы видно, как при увеличении экспоненты (степени двойки) увеличивается число нулей в начале мантиссы, а значит, уменьшается точность представления числа. Теперь мы произведем обратную операцию: по двоичному представлению в памяти восстановим исходное число. Для этого выведем числа аналитически (в виде дробей) и воспользуемся калькулятором с фиксированной точностью вычислений bc(1):

#include <iostream>
#include <bitset>
#include <cmath>

void print(float f) {
    std::bitset<32> bits(*reinterpret_cast<uint32_t*>(&f));
    std::cout << "scale=20\n";
    std::cout << "(2^(0";
    for (int i=0; i<=7; ++i) {
        if (bits[23+i]) {
            std::cout << " + " << bits[23+i]*(1<<i);
        }
    }
    std::cout << " - 127)) * (1";
    for (int i=1; i<=23; ++i) {
        if (bits[23-i]) {
            std::cout << " + " << bits[23-i] << '/' << (1<<(i));
        }
    }
    std::cout << ")";
    std::cout << '\n';
}

int main() {
    std::cout << "scale=20\n";
    for (int i=1; i<=10; ++i) {
        print(float(1<<i) + 1.f/3.f);
    }
}

Далее перенаправим вывод этой программы на вход калькулятора bc и получим

   2.33333325386047363280
   4.33333349227905273436
   8.33333301544189453120
  16.33333396911621093744
  32.33333206176757812480
  64.33333587646484374976
 128.33332824707031249920
 256.33334350585937499904
 512.33331298828124999680
1024.33337402343749999616

Здесь также видно, что с увеличением степени двойки мы терям точность, и даже при минимальной степени двойки точность не превышает шести десятичных разрядов после запятой. Итого, мы узнали, что точность уменьшается с увеличением числа, то есть является относительной величиной, и она ограничена количеством двоичных разрядов числа, которое задается типами float и double.

Тот факт, что погрешность является относительной, а не абсолютной, влияет на свойства чисел и операций над ними. Так операции сложения и умножения в компьютере не являются ассоциативными, а для минимизации погрешности следует стремиться к операциям над числами одинакового порядка. Покажем это на примерах. В примерах операторы, обведенные в кружок, обозначают операции на числами с плавающей точкой, а все остальные операторы обозначают точные операции.

Вслед за Голдбергом рассмотрим формулу $x^2 - y^2 = (x-y)(x+y)$, которую можно реализовать на компьютере либо через два умножения и одно вычитание, либо через вычитание, сложение и умножение. Обозначим погрешность вычитания как $\delta_1 = \frac{(x \ominus y) - (x-y)}{x-y}$. Выражая отсюда вычитание чисел с плавающей точкой, получаем $x \ominus y = (x-y)(1+\delta_1)$. Аналогично получаем формулы для сложения и умножения: $x \oplus y = (x+y)(1+\delta_2), x \otimes y = xy(1+\delta_3)$. Теперь мы можем оценить погрешность исходных формул:

$(x \otimes x) \ominus (y \otimes y) = (x^2 (1 + \delta_4) - y^2 (1 + \delta_5)) (1 + \delta_6) = ((x^2-y^2) (1+\delta_4) + (\delta_4-\delta_5) y^2) (1+\delta_6), \\ (x \ominus y) \otimes (x \oplus y) = (x^2-y^2) (1+\delta_7)(1+\delta_8)(1+\delta_9).$

Из полученных формул видно, что если x и y близки, то первая формула дает гораздо большую погрешность, чем вторая.

В реальных задачах часто встречается суммирование большого количества чисел. Нетрудно догадаться, что простейшая его реализация приведет к проблемам с погрешностью: порядок переменной-аккумулятора быстро станет отличным от порядка элемента массива. Для уменьшения погрешности существует несколько методов.

Один из таких методов — это попарное суммирование. Действительно, если предположить, что в массиве содержатся числа одного порядка, то рекурсивное суммирование их по парам означает, что на каждом этапе будут суммироваться числа одного порядка, а значит, погрешность будет меньше, чем в случае переменной-аккумулятора.

Другой метод, именуемый суммирование Кэхена, использует прямой подход для решения проблемы. В нем ошибки суммирования чисел различных порядков компенсируются за счет дополнительных операций и переменных. На псевдокоде этот алгоритм записывается следующим образом.

s = 0
c = 0
for i=1,n
  y = x[i] - c
  t = s + y
  c = (t - s) - y
  s = t

Здесь используется корректирующий коэффициент c, который на итерации i инициализируется битами, потерянными при суммирование чисел разных порядков, а на итерации i+1 вычитается из нового элемента массива, тем самым корректируя сумму.

Аналогичные формулы с корректирующими коэффициентами существуют для алгоримов, основанных на суммировании. Так для вычисления математического ожидания и дисперсии выборки используется метод Велфорда:

$\overline{x}_n = \overline{x}_{n-1} + \frac{x_n - \overline{x}_{n-1}}{n}, \\ M_n = M_{n-1} + (x_n - \overline{x}_{n-1}) (x_n - \overline{x}_n), \\ \sigma^2_n = \frac{M}{n}.$

Погрешность, связанная с переполнением, также может возникать в реальных задачах. Примером служит формула вычисления длины геометрического вектора: $\left|\vec{v}\right| = \sqrt{x^2 + y^2}$. Если мы попытаемся вычислить длину прямо по этой формуле, то если квадраты x или y превышают максимально допустимое число, которое может хранить выбранный нами тип данных, то произойдет переполнение. При этом длина будет меньше максимально допустимого числа. Для решения это проблемы компоненты вектора нормализуются на максимальную компоненту: $m = \text{max}\{|x|,|y|\}, \left|\vec{v}\right| = m\sqrt{\left(\frac{x}{m}\right)^2 + \left(\frac{y}{m}\right)^2}$.

🌊🌊🌊

Подведем итог. Погрешность является неотъемлемой частью численных методов. Погреность математических моделей часто является неустранимой, и повлиять на нее можно, только изменив модель на другую. Погрегшность численного метода регулируется параметрами, однако, она не может быть меньше погрешности компьютера. Погрешность компьютера зависит числа разрядов, используемых для чисел с плавающей точкой, а также от порядка операций над этими числами. Чтобы минимизировать эту погрешность, операции нужно стремиться производить над близкими по величине числами. При агрегации (суммировании) большого количества чисел, возникает проблема накопления ошибки, для решения которой используются специфичные для каждого случая алгоритмы. Наконец, погрешность, возникающая из-за переполнения, хоть и редко, на все таки встречается в реальных задачах. Эта погрешность уменьшается за счет масштабирования (нормализации) чисел.

Задания

Линейная интерполяция 1 балл

Для линейной интерполяции между двумя скалярными величинами a и b используют одну из двух следующих функций.

float lerp_v1(float a, float b, float t) {
  return a + t*(b - a);
}
float lerp_v2(float a, float b, float t) {
  return (1.f-t)*a + t*b;
}

Используя формулы Голдберга, докажите, что

• первая функция дает точный результат при a==b и может дать неточный результат при t==1.f;
• вторая функция дает точный результат при t==1.f и может дать неточный результат при a==b.

Вычисление полиномов 1 балл

Полиномы вида $p(x) = a_0 + a_1 x + a_2 x^2 + \ldots + a_n x^n$ часто используются в численных методах.

• Напишите функцию polynomial на C++, которая вычисляет их с помощью функции std::fma. Прототип функции должен выглядеть следующим образом.

  // a - массив коэффициентов
  // n - длина массива коэффициентов a
  float polynomial(float x, const float* a, int n);
  

• Используя формулы Голдберга, напишите формулу с погрешностью для полинома третьей степени $a_0 + a_1 x + a_2 x^2 + a_3 x^3$, вычисленного с помощью std::fma.

Суммирование Кэхена 1 балл

Напишите функцию на C++, которая реализует суммирование Кэхена для массива чисел с плавающей точкой. Сравните погрешность этой функции с погрешностью функции, использующей переменную-аккумулятор. Удостоверьтесь, что компилятор не оптимизирует суммирование Кэхена.

float kahan_sum(const float* x, int n);

Попарное суммирование на SIMD 2 балла

Напишите функцию на C++, которая реализует попарное суммирование массива чисел с плавающей точкой, и повысьте его эффективность с помощью директивы #pragma omp simd. Входной массив можно перезаписывать. Сравните погрешность этой функции с погрешностью функции, использующей переменную-аккумулятор. Сравните время работы этой функции со временем работы функции, использующей переменную-аккумулятор. Для того чтобы компилятор использовал векторные инструкции, укажите опции -O3 -march=native -fopenmp.

float pairwise_sum_simd(float* x, int n);

Статистика 1 балл

Напишите класс Statistics, который вычисляет минимальное, максимальное, сумму и среднее значение выборки, а также дисперсию и количество элементов. Среднее и дисперсия нужно вычислить с помощью метода Велфорда. Класс должен иметь следующий прототип (поля можно добавлять любые).

class Statistics {
public:
  void update(float x);            // добавить новый элемент
  int count() const noexcept;
  float min() const noexcept;
  float max() const noexcept;
  float sum() const noexcept;
  float mean() const noexcept;     // среднее
  float variance() const noexcept; // дисперсия
};

Длина вектора в $n$-мерном пространстве 1 балл

Напишите функцию, которая вычисляет длину геометрического вектора в пространстве любой размерности. Для того чтобы избежать переполнения, вычисляйте максимальный по модулю элемент на каждой итерации цикла, который суммирует элементы, и нормируйте текущую сумму заново, если максимальный элемент поменялся. Повышать точность суммирования другим способом не нужно. Заранее сканировать массив для поиска максимального по модулю элемента также не нужно.

float length(const float* x, int n);

Видео

2023

2022

Доска

2023

2022