Содержание

Случайный поиск
Метод LiPO
Генетические алгоритмы
Гибридные методы
Задания
Видео

§ 4. Глобальная оптимизация

Случайный поиск

Наиболее простым методом оптимизации невыпуклых функций является случайный поиск (или случайное блуждание). На каждой итерации этого метода псевдослучайным образом выбирается новая точка из подобласти определения функции, в выбранной точке вычисляется целевая функция, и, если ее значение в этой точке меньше значения в предыдущем приближении, то она выбирается за новое приближение. Выбор новой точки может происходить сколь угодно сложным способом, один из распространненых способов — выбор точки из гиперсферы определенного радиуса с центром в точке текущего приближения решения задачи. Один из алгоритмов выбора точки из гиперсферы — это алгоритм Марсаглии:

\vec{p} = \frac{1}{\sqrt{x^2 + y^2}}\left[\begin{array}{l}x\\y\end{array}\right].

Здесь $\vec{p}$ — псевдослучайный вектор, равномерно распределенный по поверхности сферы единичного радиуса, $x, y$ — псевдослучайные числа, нормально распределенные на промежутке $[0,1]$ .

Несмотря на то что для случайного поиска, как правило, невозможно определить скорость сходимости, он работает для любых функций: выпуклых и невыпуклых, с разрывами и без, с функциями, для которых существуют производные и для которых не существуют. Также этот метод легко ускорить на многопроцессорной машине, запустив поиск параллельно в нескольких потоках. У метода существуют различные модификации с которыми мы познакомимся в следующих разделах.

Метод LiPO

Этот метод является модификацией случайного поиска, в которой для выбора нового приближение используется правило, основанное на константе Липшица. Функцией Липшица (или отображением Липшица) называется функция, которая удовлетворяет условию Липшица:

\forall x \, \forall y \, \exists L \geq 0: \left|f(x)-f(y)\right| \leq L\left|x-y\right|.

Любая непрерывно дифференцируемая функция является Липшицевой, однако обратное утверждение в общем случае неверно. Идея метода заключается в том, чтобы среди псевдослучаных точек выбрать только те точки, верхняя граница которых (заданная условием Липшица) превышает текущее приближение.

\underset{i=1...t}{\text{min}}\left\{f(\vec{x}_i) + L\left|\vec{x}_{t+1}-\vec{x}_i\right|\right\} \geq \underset{i=1...t}{\text{max}}\left\{f(\vec{x}_i)\right\}.

Здесь $f$ — оптимизируемая функция, $L$ — константа Липшица, $x_{t+1}$ — новое приближение, выбранное псевдослучайным образом, $x_i$ — старые приближения. В качестве константы Липшица можно взять некоторое малое число или же использовать модификацию метода под названием AdaLiPO, в которой значение константы обновляется на каждом шаге по следующей формуле.

L_{i+1} = \text{inf}\!\left\{ L_i: \underset{i\neq{}j}{\text{max}} \frac{\left|f(\vec{x}_i)-f(\vec{x}_j)\right|} {\left|\vec{x}_i-\vec{x}_j\right|} \leq L_i \right\}

Выбранная таким образом константа соответствует наибольшему наклону оптимизируемой функции.

В качестве нового приближения выбирается не псевдослучайная точка, а точка, в которой верхняя граница принимает максимальное значение. Верхняя граница вычисляется по формуле

U(x) = \underset{i = 1...t}{\text{min}}\left\{f(x_i) + k\left|x - x_i\right|\right\}.

Это кусочно определенная функция, которая из каждой точки $\vec{x}_i$ расходится прямыми под углом, определяемым константоя Липшица. В точках пересечения прямых находятся локальные максимумы этой функции. Точка пересечения для прямых, исходящих из точек $\vec{x}_i$ и $\vec{x}_j$ определяется из уравнения

f(\vec{x}_i) + k\left|\vec{x} - \vec{x}_i\right| = f(\vec{x}_j) + k\left|\vec{x} - \vec{x}_j\right| \Rightarrow x = \frac{1}{2k}\left(f(\vec{x}_j) - f(\vec{x}_i)\right) + \frac{1}{2}\left(\vec{x}_i + \vec{x}_j\right).

Таким образом, новая точка на каждой итерации выбирается псевдослучайным образом из списка точек, в которых верхняя граница превышает текущее приближение глобального максимума функции. Это и делает алгоритм более эффективным, чем случайный поиск.

В своей статье авторы метода доказывают, что за счет продуманного выбора нового приближения, их метод более эффективен, чем случайный поиск. Метод разрабатывался для оптимизации гиперпараметров алгоритмов машинного обучения, но может применяться к любым липшецевым функциям.

Генетические алгоритмы

Это эвристические методы оптимизации, основанные на принципах эволюции биологических видов: селекции, мутации, скрещивании и т.п. Генетичский алгоритм заключается в следующем.

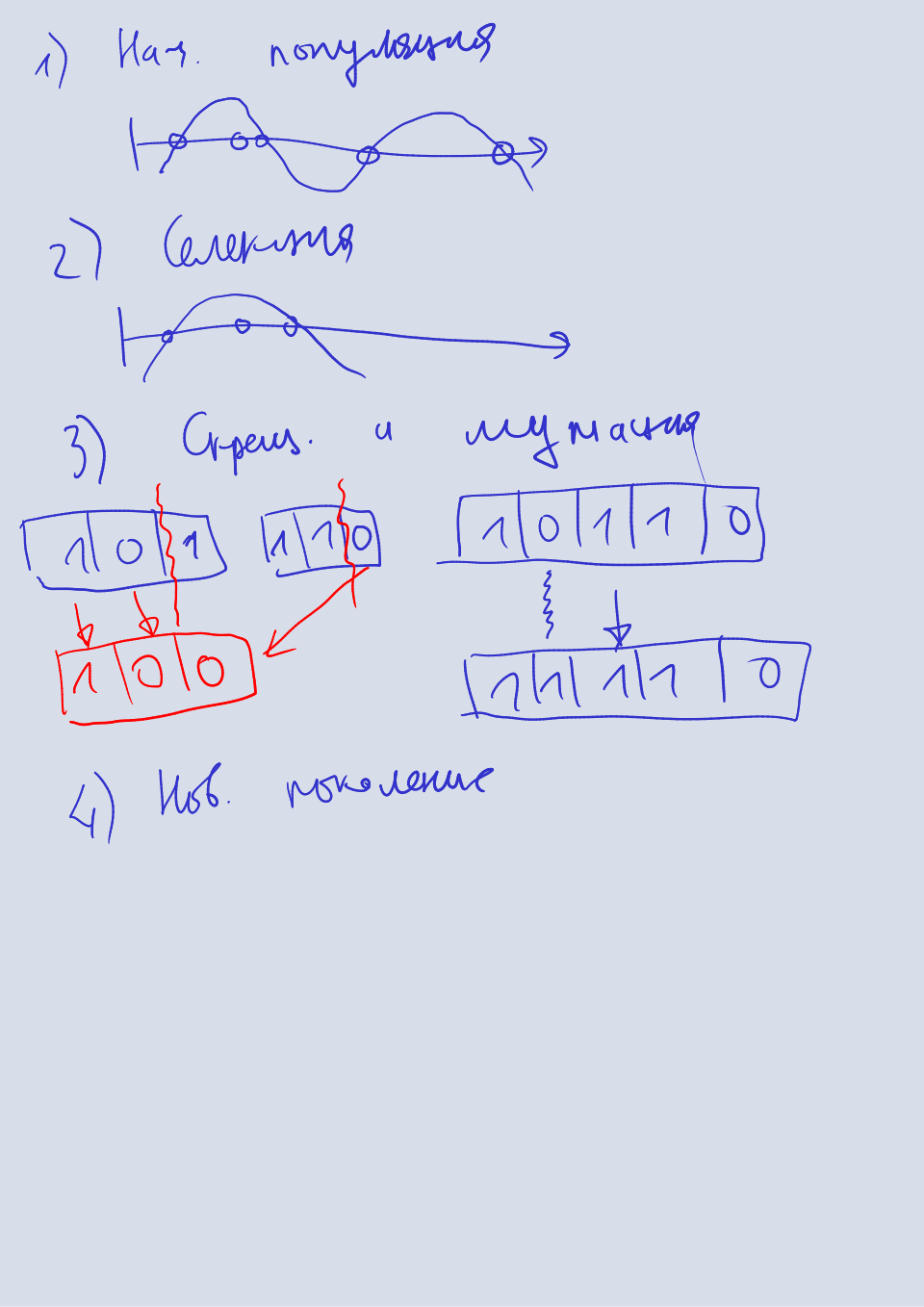
Формирование начальной популяции.
Селекция.
Скрещивание и мутация.
Формирование нового поколения.

Последние три этапа повторяются до тех пор, пока не получена популяция с требуемыми параметрами. Это общий подход, который применим не только к методами оптимизации. Теперь расшифруем каждый этап в случае оптимизации.

На этапе формирования начальной популяции псевдослучайным образом генерируются аргументы целевой функции. В рамках генетических каждая особь из популяции представляет собой вектор генов (битовую строку). Чтобы полчить битовую строку, каждый вещественный аргумент целевой функции преобразуется в беззнаковое целое число, которое показывает его положение в области определения функции. При этом область ограничивается некоторым минимальным и максимальным значением, как и случае других методов оптимизации. Затем это беззнаковое число преобразуется в набор бит, используя код Грея. Код Грея традиционно применяется в генетических алгоритмах, поскольку в нем комбинации бит, идующие друг за другом (то есть когда соответствующие им числа упорядочены по возрастанию или убыванию), отличаются лишь на один бит. Это свойство полезно, поскольку с кодом Грея мутации выбирают близкие по значению числа. Преобразование беззнакового числа в код Грея и обратно показано в следующей программе.

unsigned int number_to_gray(unsigned int n) {
    return n ^ (n >> 1);
}

unsigned int gray_to_number(unsigned int g) {
    unsigned int n = 0;
    for (; g!=0; g >>= 1) { n ^= g; }
    return n;
}

Мы получили начальную популяцию, которая представляет собой набор особей, каждая из которых является набором бит, который соответствует комбинации аргументов целевой функции. Теперь мы переходим к этапу селекции. На этом этапе из текущей популяции выбираются наиболее приспособленные особи. В рамках математической оптимизации это означает выбор фиксированного числа комбинаций аргументов с самым высоким (низким) значением целевой функции. Такая селекция называется турнирной.

Далее мы переходим этапу скрещивания и мутации. На этом этапе мы для каждой пары приспособленных особей (пары могут выбираться произвольно) создаем две дочерних особи: для каждой дочерней особи произвольно выбирается граничный бит, и все биты до него копируются из первого родителя, остальные биты копируются из второго родителя. Эта операция называется скрещиванием. Далее происходит мутация получившихся особей путем обращения значений произвольно выбранных бит.

Финальным этапом метода является формирование нового поколения, в которое входят все дочерние особи. Если требуемая точность не достигнута, то алгоритм продолжается с этой новой популяцией, которая дополняется недостающим количеством особей, генерируемых псевдослучайным образом.

Каждая операция в генетических алгоритмах имеет математическую интерпретацию. Мутация позволяет выбрать точки, которые близки по значениям к текущему приближению, это основной инструмент поиска локального экстремума. Скрещивание позволяет выбрать точки, которые сильно различаются по значеним по сравнению с текущим приближением, то есть совершить прыжок из оврага, в который нас загнала мутация. Наконец, селекция позволяет нам отсеять точки, которые не являются глобальным экстремумом.

Скорость и условия сходимости генетических сложно доказать математически. Формально они являются разновидностью случайного поиска, в котором выбор новых точек происходит по принципу естественного отбора. Преимуществом данного метода является высокий уровень параллелизма, что ускоряет поиск на многопроцессорной машине и кластере. Целесообразность применения генетических алгоритмов в реальных задачах вызывает вопросы, однако их изучение позволяет расширить кругозор.

Гибридные методы

Основными этапами многих методов глобальной оптимизации являются

разбиение области определения функции на подобласти,
исключение подобластей, в которых точно не может быть экстремума,
поиск экстремума в оставшихся подобластях.

Для каждого из этапов можно применять разные методы. Например, для разбиения области можно разделить ее на несколько частей, а можно псевдослучайным образом сгенерировать новые точки, которые разделят исходную область на несколько подобластей. Для исключения подобластей можно использовать производную функции, а можно использовать условие Липшица. Наконец, для поиска экстремума внутри подобласти можно использовать один из методов локальной оптимизации, а можно выбрать одну из точек, в которых значение функции уже было посчитано во время этапа разбиения. Такая гибкость позволяет выбирать наиболее эффективные методы для конкретной задачи, и такой подход называется гибридным.

🌊🌊🌊

Мы изучили методы локальной и глобальной оптимизации и узнали, что их главным отличием друг от друга являются требования, которые они предъявляют к оптимизируемым или целевым функциям, а также скорость сходимости. Исходя из опыта автора, можно дать следующие общие рекомендации.

Использовать стохастические методы для фукнций больших размерностей, для которых невозможно доказать наличие производных в каждой точке или липшецевость.
Использовать детерминистические методы, которые не требуют производных для функций средней размерности.
В остальных случаях использовать наиболее удобный детерминистический метод с производной или без, в зависимости от условий задачи.

Возможен и гибридный подход, в котором сначала используется метод поиска глобального минимума, а затем используется метод поиска локального минимума для уточнения решения. Также не стоит забывать, что все методы оптимизации также являются методами поиска корней нелинейных уравнений и их систем.

Задания

LiPO1 балл

Найдите минимум функции Растригина с помощью метода случайного поиска и метода LiPO. Сравните скорость их сходимости (количество вызовов целевой функции).

Генетические алгоритмы2 балла

Найдите минимум функции Растригина с помощью метода случайного поиска и метода на основе генетических алгоритмов. Сравните скорость их сходимости (количество вызовов целевой функции).

Решение уравнений2 балла

Найдите все корни функции $\sin(x)$ с помощью гибридного метода оптимизации. Для этого реализуйте гибридный метод оптимизации, который использует деление области на равные части, условие Липшица для исключения частей, в которых корней быть не может, и метод бисекции для локальной оптимизации внутри частей. Сравните скорость сходимости этого метода с методом случайного поиска (количество вызовов целевой функции).

Решение уравнений v22 балла

Используйте параллельные потоки для поиска решения уравнения гибридным методом и методом случайного поиска. Постройте таблицу ускорения: зависимость времени работы от количества потоков — для каждого из методов.