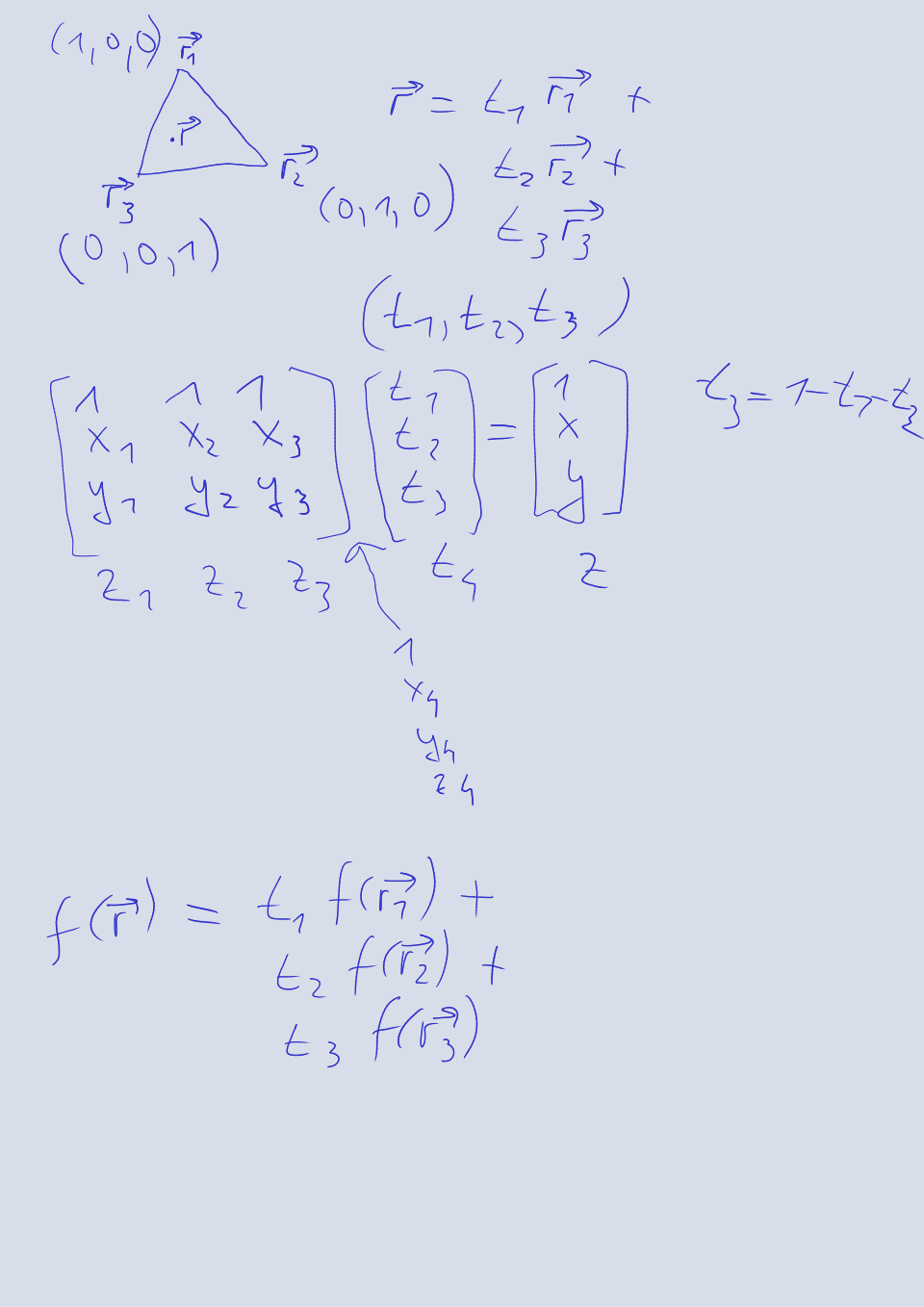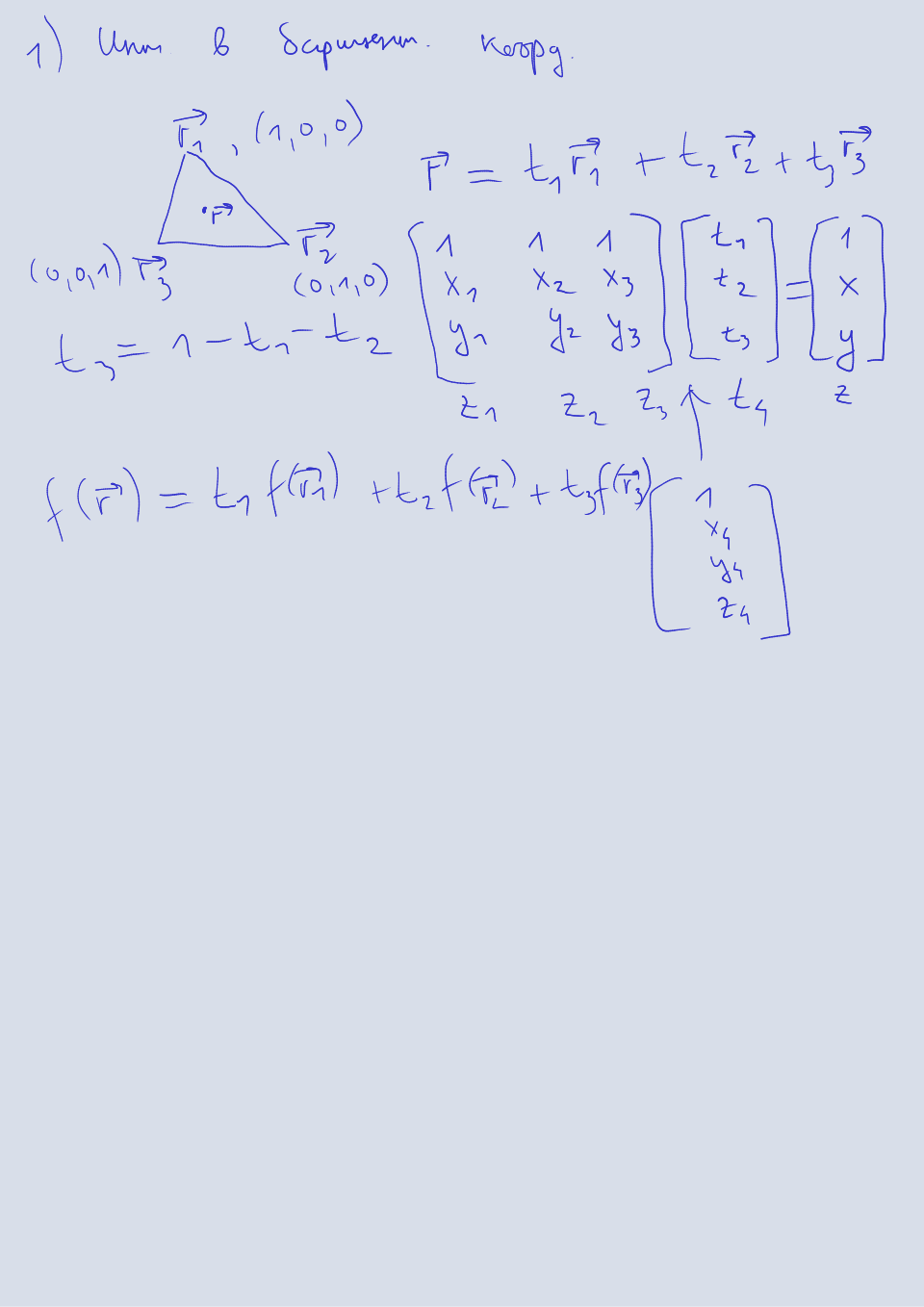Содержание

Интерполяция в барицентрических координатах
Интерполяция методом ближайших соседей
Интерполяция радиально-базисными функциями
Задания
Видео

§ 6. Интерполяция на нерегулярной сетке

Интерполяция в барицентрических координатах

Барицентрическими координатами называется тройка чисел $(t_1,t_2,t_3)$ , которые соответствуют массам, расположенных в вершинах треугольника. Если сумма этих координат равна единице, то они называются однородными и однозначно определяют координаты точки внутри треугольника:

\vec{r} = t_1\vec{r}_1 + t_2\vec{r}_2 + t_3\vec{r}_3

Здесь $\vec{r}_{1,2,3}$ — это декартовы координаты вершин треугольника. Барицентрические координаты вершин треугольника равны $(1,0,0)$ , $(0,1,0)$ , $(0,0,1)$ соответственно. Из-за того что сумма однородных барицентрических координат равна единице, третья координата всегда зависит от остальных.

Для того чтобы вычислить значение функции в любой точке внутри треугольника по известным значениям этой функции в вершинах треугольника, используется формула

f(\vec{r}) \approx t_1 f(\vec{r}_1) + t_2 f(\vec{r}_2) + t_3 f(\vec{r}_3).

Для вычисления барицентрических координат точки по декартовым координатам вершин используется система уравнений

\left[\begin{array}{lll} 1 & 1 & 1 \\ x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ \end{array}\right] \left[\begin{array}{l}t_1\\t_2\\t_3\end{array}\right] = \left[\begin{array}{l}1\\x\\y\end{array}\right],

решение которой записывается как

t_1 = \frac{1}{d}\left((y_2-y_3)(x-x_3) + (x_3-x_2)(y-y_3)\right), \\ t_2 = \frac{1}{d}((y_3-y_1)(x-x_3) + (x_1-x_3)(y-y_3)), \\ t_3 = 1 - t_1 - t_2, \\ d = (y_2-y_3)(x_1-x_3) + (x_3-x_2)(y_1-y_3).

Барицентрические координаты обобщаются на тетраэдры путем добавления координаты $z$ и коорданты $t_4$ в вышеописанные уравнения. После этого координаты $(t_1,t_2,t_3,t_4)$ однозначно описывают положение точки внутри тетраэдра.

Интерполяцию в барицентрических координатах можно считать обобщением линейной интерполяции на нерегулярные треугольные сетки. Этот метод широко применяется в задачах, где используются трехмерные модели объектов, которые чаще всего описываются именно такими сетками.

Интерполяция методом ближайших соседей

Для нерегулярных сеток (облаков точек) применяют методы, основанные на поиске $n$ ближайших соседних точек и вычислении на их основе взвешенного среднего значения функции в заданной точке.

f(\vec{x}) \approx \sum\limits_{i=1}^{n} w_i f(\vec{x}_i).

В качестве весовой функции используют обратное расстояние:

w_i=\left|\vec{x}-\vec{x}_i\right|^{-p}, \quad p \geq 1.

Интерполяция радиально-базисными функциями

В данном методе функция интерполируется с помощью взвешенной суммы радиально-базисных функций.

f(\vec{x}) \approx \sum\limits_{i=1}^{n} w_i \phi(|\vec{x}-\vec{x}_i|).

Радиально-базисной функцией называется функция, которая зависит от расстояния от точки $\vec{x}$ до какой-либо фиксированной точки. В данном методе в качестве фиксированных точек выбираются $n$ ближайших соседей. Веса определяются из системы уравнений

\left[\begin{array}{llll} 1 & \phi(|\vec{x}_2-\vec{x}_1|) & \ldots & \phi(|\vec{x}_n-\vec{x}_1|) \\ \phi(|\vec{x}_1-\vec{x}_2|) & 1 & \ldots & \phi(|\vec{x}_n-\vec{x}_2|) \\ \vdots & \vdots & \ddots & \vdots \\ \phi(|\vec{x}_1-\vec{x}_n|) & \ldots & \ldots & 1 \\ \end{array} \right] \left[\begin{array}{l}w_1\\w_2\\\vdots\\w_n\end{array}\right] = \left[\begin{array}{l} f(\vec{x}_1)\\f(\vec{x}_2)\\\vdots\\f(\vec{x}_n) \end{array}\right].

Как правило, количество ближайших соседей фиксировано и невелико, а это значит, что для системы можно получить решение в явном виде.

В качестве радиально-базисной функции в зависимости от задачи выбирают

функцию Баттерворта $\phi(\vec{x}-\vec{x}_i) = \frac{1}{1 + \left(\frac{|\vec{x}-\vec{x}_i|}{\sigma}\right)^{2p}}$ ;
функцию Гаусса $\phi(\vec{x}-\vec{x}_i) = \exp\left(-(\epsilon|\vec{x}-\vec{x}_i|)^2\right)$ ;
другие аналогичные функции.

Задания

Барицентрические координаты1 балл

Перед вами поверхность, заданная дискретно массивом $128\times{}128$ точек. Напишите программу, которая вычисляет координату $z$ поверхности в любой точке $(x,y)$ внутри поверхности с помощью барицентрической интерполяции. Для этого разделите поверхность на прямоугольные области (сетку), а каждый прямоугольник на два треугольника. Затем используйте один из треугольников для интерполяции. Проверить себя можно с помощью программы Gnuplot.

splot 'surface.xyz' # нарисовать поверхность
splot 'surface.xyz', 'mypoints.xyz' # нарисовать поверхность + интерполированные точки

Радиально-базисные функции2 балла

Выполните первое задание, используя интерполяцию радиально-базисными функциями по четырем точкам, которые обрамляют прямоугольник, в который попала интерполируемая точка. Веса можно вычислить как численно, так и аналитически (с помощью Mathics). В качестве радиально-базисной функции можно использовать любую подходящую функцию.

Точки пересечения сложных фигур (3D)3 балла

Найдите точки пересечения треугольника и поверхности в трехмерном пространстве. Треугольник может иметь любую ориентацию в пространстве, а под поверхностью должна быть одна или две вершины (но не три). Вычислите координаты точек пересечения с помощью метода бисекции, интерполируя точки на поверхности с помощью барицентрических координат или радиально-базисных функций.