§ 5. Интерполяция на регулярной сетке

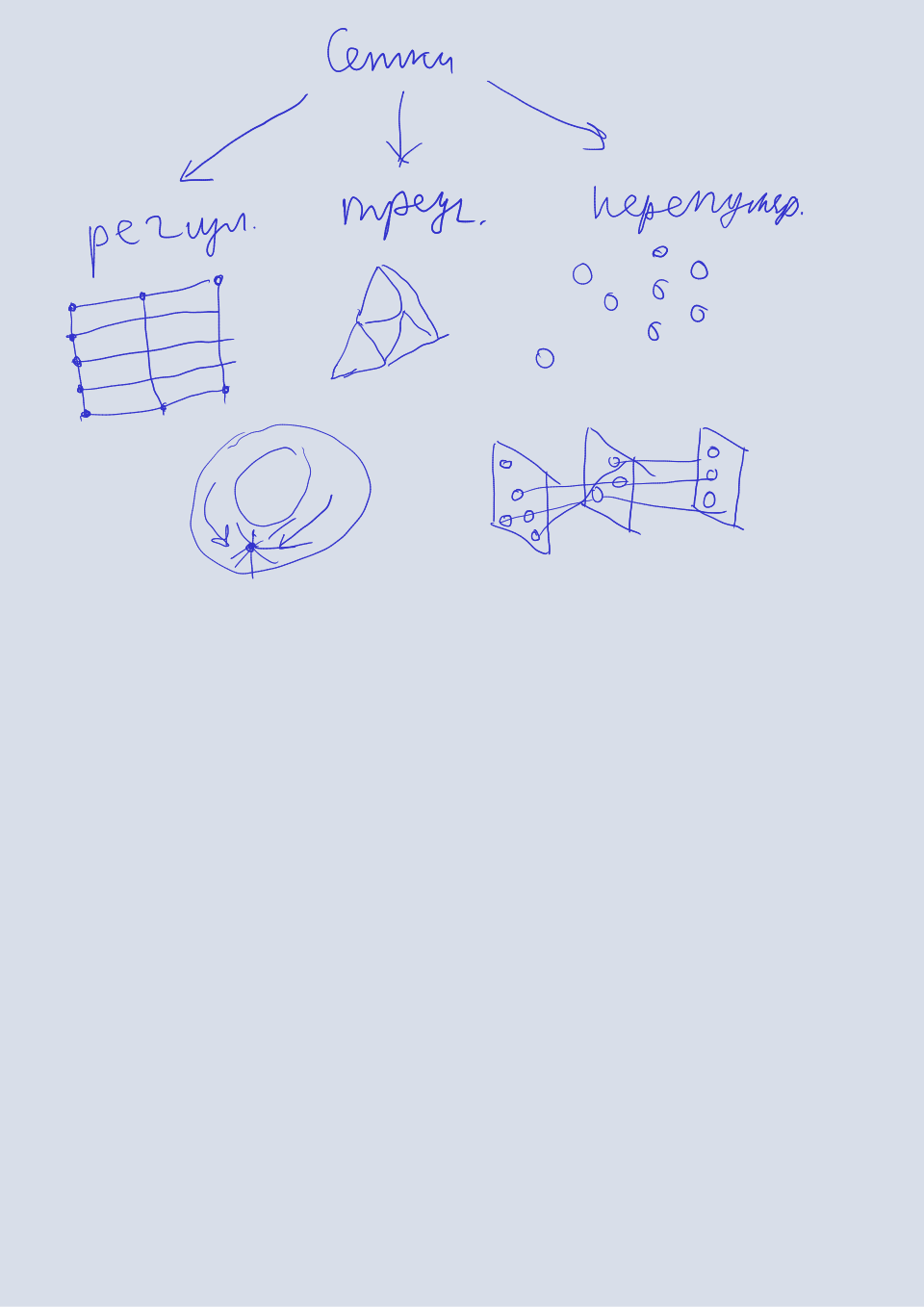
Виды сеток

Регулярной сеткой называется сетка, каждый элемент которой является отрезком (в случае одного измерения), параллелограммом (в случае двух измерений) или параллелепипедом (в случае трех).

Нерегулярной треугольной сеткой называется сетка, каждый элемент которой является треугольником (в случае двух измерений) или тетраэдром (в случае трех измерений).

Нерегулярной сеткой называется сетка, в которой нет какой-либо структуры. Иногда такие сетки называют облаками точек.

Обобщение понятия сетки на четыре и более измерений возможно, однако легко объяснимой терминологии для фигур-элементов не сущестует. Вид сетки определяет, какой метод интерполяции может быть к ней применен.

Математическая постановка задачи

Интерполяция — это поиск значений функции в промежуточных точках по известным значениям функции в окружающих точках. Математически это записывается как

То есть для функции $f_i$, значения которой известных лишь в точках $x_i$, мы находим интерполирующую ее функцию $F$ (интерполянт), которая определена во всех промежуточных точках, а в точках $x_i$ ее значение совпадает с исходной функцией.

Сглаживанием называется аппроксимация дискретно заданной функции некоторой другой функцией, которая более гладкая по сравнению с исходной функцией, а также игнорирует отдаленные точки (шум). Как правило, сглаживающая функция не проходит через точки, в которых определена исходная функция, а целью сглаживания является нахождение гладкой аппроксимации зашумленных данных.

Понятия интерполяции и сглаживания не являются математически строгими. Соответствующие методы схожи, однако находятся на противоположных концах спектра: интерполянт всегда проходит через точки, в которых задана функция, а сглаживающая функция проходит по некоторой усредненной с учетом окружающих известных точек кривой. Общим термином для этих двух методов в одномерном пространстве является приближение с помощью кривых. Если же мы хотим найти значения функции в точках, которые не окружены точками, в которых значения функции известны, то такие методы называются экстраполяцией.

Линейная интерполяция

Этот вид интерполяции основан на приближении функции с помощью отрезков, которые соединяют соседние точки, в которых значение функции известно. В промежуточных точках функция вычисляется по формуле

В двухмерном случае формула запишется как

В $n$-мерном случае формула запишется как

Здесь векторные индексы означают выбор дискретных точек, а скалярные индексы означают выбор компоненты вектора, $\vec{0}$ — вектор нулей, $\vec{1}$ — вектор единиц.

Несмотря на то что линейная интерполяция является наименее точной, она также является самым быстрым методом интерполяции, из-за чего широко применяется в компьютерной графике. В частности, в видеокартах двух- и трехмерная интерполяция текстур выполняется автоматически на аппаратном уровне.

Интерполяция полиномами Лагранжа

Основная идея полиномиальной интерполяции заключается в аппроксимации исходной функции полиномом заданной степени, вычислению коэффициентов этого полинома и затем вычислению по формуле полинома значений функций в промежуточных точках. Для этого мы приравниваем полином значению функции в известных точках и решаем систему уравнений относительно коэффициентов полинома:

Решая эту систему уравнений, получаем следующую формулу для полинома:

Эта форма записи полинома называется полиномом Лагранжа. При $n=1$ эта формула сводится к формуле линейной интерполяции. Таким образом, линейная интерполяция является частным случаем полиномиальной, когда степень полинома равна единице.

Интерполяция полиномами Ньютона

Идея заключается в аппроксимации функции полиномами Ньютона, причем в каждой последующей известной точке степень полинома отличается на единицу.

Это приводит к системе уравнений

Система решается итеративно, сначала находится коэффициент $a_0$, затем все остальные. По сравнению с полиномами Лагранжа при добавлении новых точек, в которых значение исходной функции известно, прежние коэффициенты полиномов Ньютона не нужно пересчитывать.

Интерполяция сплайнами

Сплайн — кусочно заданная полиномиальная функция. Эта функция состоит из функций-фрагментов, каждый из которых определен на своем промежутке, а на стыках промежутков обычно выполняется условие равенства производных. Такой подход позволяет решить проблему осцилляции полиномов высокой степени, заменив их полиномами небольших степеней и дополнительным условием равенства производных этих полиномов на границах промежутка, которое обеспечивает гладкость функции.

Кубический сплайн (общий случай)

Запишем систему уравнений для одномерного кубического сплайна (сплайна третьего порядка). Нам известно значение функции в $n+1$ точках $f(x_1), \ldots, f(x_{n+1})$. Каждый интервал интерполируется полиномом третьей степени $p_i(t) = a_i + b_i t + c_i t^2 + d_i t^3$, где $t \in [0,1]$ — параметр, а $i=1,\ldots,n$. На концах интервалов полином запишется как

а его производная запишется как

Решая последние четыре уравнения относительно коэффициентов, получим

Полученных значений коэффициентов достаточно, чтобы произвести интерполяцию, при условии, что известны производные интерполируемой функции. Если же производные неизвестны, то в общем случае их можно найти следующим образом.

Приравняем значения функции, а также ее первые и вторые производные на граничных точках соседних интервалов:

На левой и правой границах области определения функции обнулим вторые производные:

Из полученных уравнений составляем систему

Эта система является трехдиагональной и решается стандартными для таких систем методами. На практике же производные интерполируемой функции проще всего аппроксимировать, а не вычислять каждый раз из этой большой и сложной системы уравнений.

Кубический сплайн Эрмита

Эти сплайны не используют полином Эрмита, а только названы в честь этого ученого. Здесь производные аппроксимируются конечными разностями (подробный разговор о которых пойдет в последующих разделах, а здесь представлены готовые формулы). Полином для каждого промежутка записывается как

Здесь $h$ — это базисные функции, $m_i$ — аппроксимации производных, которые записываются одним из следующих способов.

где $t \in [0,1]$ — параметр. Первая формула является средним значением производных двух соседних интервалов, записанных в виде конечных разностей. Вторую формулу называют сплайнами Катмалла—Рома.

Одномерные кубические сплайны обобщаются на двухмерный случай путем аппроксимации каждой линии сетки отдельным сплайном: сначала идет интерполяция по координате $x$, для чего строится одномерный сплайн для каждой строчки сетки, затем из получившихся точек строится еще один одномерный сплайн, который интерполирует функцию по координате $y$. Этот процесс трудоемкий, зато позволяет обобщить интерполяцию сплайнами на пространство любой размерности.

Задания

Линейная интерполяция1 балл

Аппроксимируйте функцию $\sin(x)$ с помощью линейной интерполяции и с помощью полинома Лагранжа второй степени в точках с шагом $2\pi/10$. Уменьшая шаг, найдите такую его величину, при которой точность линейной интерполяции в середине промежутка между двумя точками сопоставима с точностью интерполяции полиномом Лагранжа второй степени с исходным шагом.

Экстремумы дискретно заданной функции2 балла

Найдите все точки минимума и максимума функции $\sin(x)$, заданной дискретно в точках с шагом $2\pi/10$. (Задайте точки таким образом, чтобы на них не попадал максимум и минимум.) Для этого найдите все точки, которые меньше (больше) соседних. В найденных точках аппроксимируйте функцию полиномом Лагранжа второй степени (параболой) и определите по формуле параболы координату точки экстремума. Сравните полученные значения с реальными.

Точки пересечения сложных фигур3 балла

Найдите точки пересечения прямоугольника и синусоиды (см. картинку справа). Прямоугольник повернут на произвольный угол. Синусоида описывается функцией $\sin(x)$, заданной дискретно в точках с шагом $2\pi/10$. Вычислите координаты точек пересечения синусоиды и прямоугольника с помощью интерполяции Лагранжа второй степени и метода бисекции.

Видео

2023

2022

Доска

2023

2022