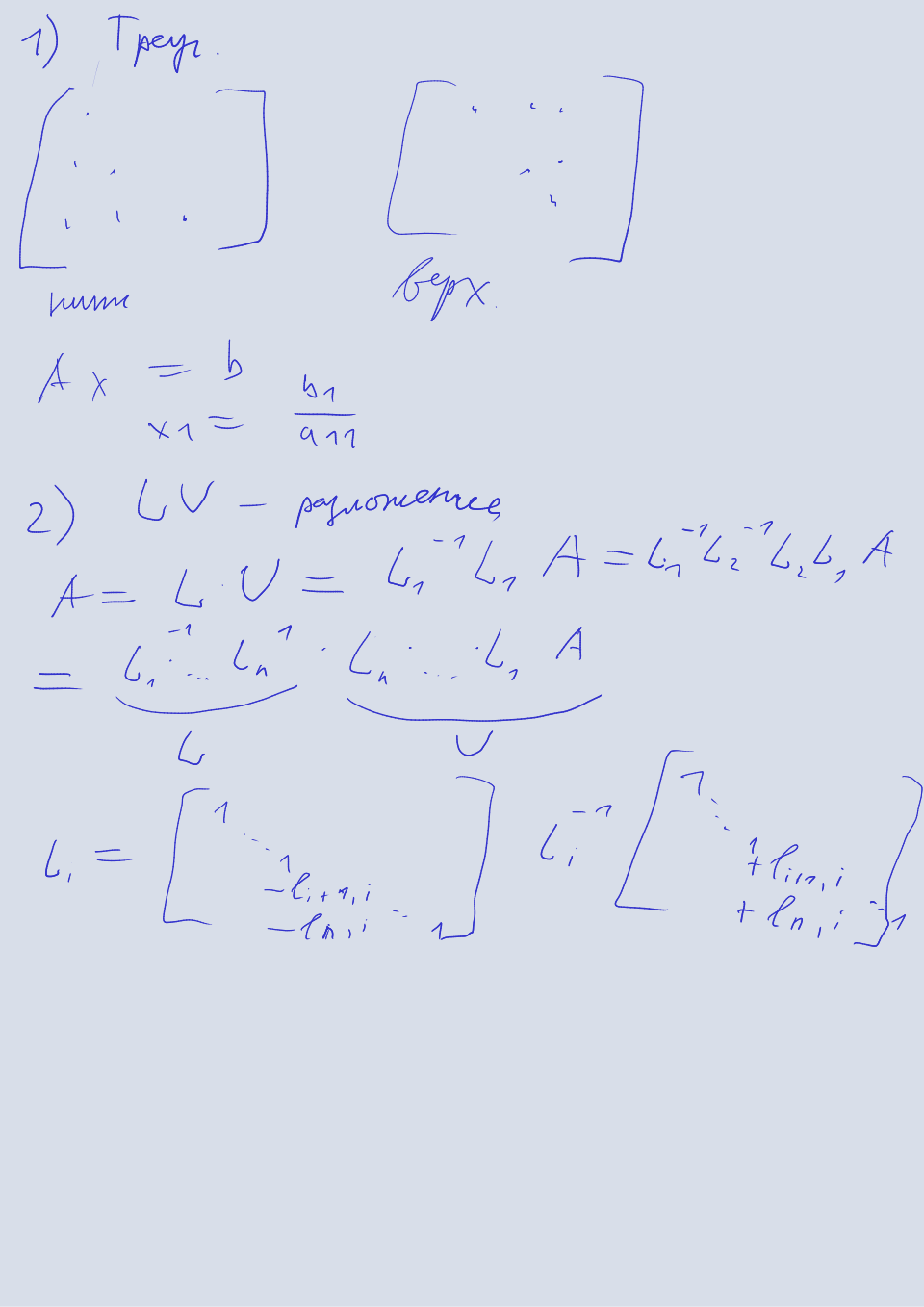Содержание

Введение
Определения
Метод прямой и обратной подстановки
Метод Гаусса
Метод прогонки
Уравнение теплопроводности (неявная схема)
Задания
Видео

§ 12. Линейные алгебраические уравнения

Введение

Линейная алгебра — это область математики, которая занимается системами уравнений. Эти системы, как правило, записываются в виде матриц коэффициентов, а их правые части — в виде векторов свободных членов. В зависимости от вида матрицы (симметричная, положительно определенная, диагональная, разреженная, прямоугольная, треугольная и т.д.) выбирается наиболее эффективный метод решения системы уравнений. Также в линейной алгебре изучаются операции над матрицами и их свойства.

Матричные и векторные вычисления эффективно отображаются на архитектуру современных компьютеров. Представление вашей задачи в векторном или матричном виде и качественный перенос этого представления в код программы повышает ее производительность по сравнению со скалярной версией за счет использования векторных регистров процессора: скалярная версия программы будет использовать только первую компоненту векторного регистра, а векторизованная версия — потенциально все компоненты.

Матричные численные методы часто являются вспомогательным инструментом, который используется при решении задач другими основными методами: везде, где возникает система уравнений, можно применить матричные численные методы. Также, эти методы являются основными в компьютерной графике и вычислительной геометрии, поскольку позволяют кратко записать преобразование координат из одной системы в другую, а также операции с геометрическимим векторами.

Определения

Линейным отображением векторного пространства $V$ на векторное пространство $W$ называется отображение $f: V \rightarrow W$ , которое удовлетворяет условиям

f(\vec{v}_1+\vec{v}_2) = f(\vec{v}_1) + f(\vec{v}_2), \quad \forall \vec{v}_1, \vec{v}_2 \in V; \\ f(\alpha \vec{v}) = \alpha f(\vec{v}), \quad \forall \alpha \in \mathbb{R}.

Матрицей называют краткую запись коэффициентов линейного отображения в табличном виде. Линейное отображение, описываемое системой уравнений

f_1' = a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n \\ \vdots \\ f_m' = a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n, \\

записывается в матричном виде как

\left[\begin{array}{l} f_1' \\ \vdots \\ f_m' \end{array}\right] = \left[\begin{array}{lll} a_{11} & \ldots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \ldots & a_{mn} \end{array}\right] \left[\begin{array}{l} x_1 \\ \vdots \\ x_m \end{array}\right].

Вектором называется элемент векторного пространства $\mathbb{R}^n$ , который задается $n$ координатами $\left[\begin{array}{l} x_1 \\ \vdots \\ x_m \end{array}\right]$ . Во многих задачах вектор можно считать частным случаем (одной колонкой или одной строчкой) матрицы для удобства. Нет консенсуса, является ли вектор по умолчанию колонкой или строчкой.

Для матриц и векторов определены привычные арифметические операции. Сложение и вычитание производится поэлементно. Умножение вектора на вектор может производиться как поэлементно, так и по более сложным формулам. Чаще всего используют следующие варианты умножения.

Скалярное произведение:
$\vec{a} \cdot \vec{b} = \sum\limits_{i=1}^n a_i b_i.$
Векторное произведение
- в трехмерном пространстве:
  $\vec{a} \times \vec{b} = \left[\begin{array}{l} a_2 b_3-a_3 b_2 \\ a_3 b_1-a_1 b_3 \\ a_1 b_2-a_2 b_1 \end{array}\right],$
- в двухмерном пространстве: $\vec{a} \times \vec{b} = a_1 b_2 - a_2 b_1.$
- в $n$ -мерном пространстве определяется с помощью тензоров.
Это произведение некоммутативно, и при перестановке аргументов знак меняется на противоположный: $\vec{a} \times \vec{b} = - \vec{b} \times \vec{a}.$
Поэлементное произведение:
$\vec{a} \circ \vec{b} = \left[\begin{array}{c} a_1 b_1 \\ \vdots \\ a_n b_n \end{array}\right].$

Умножение матрицы на матрицу записывается как

\left[\begin{array}{lll} a_{11} & \ldots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \ldots & a_{mn} \end{array}\right] \left[\begin{array}{lll} b_{11} & \ldots & b_{1p} \\ \vdots & \ddots & \vdots \\ b_{n1} & \ldots & b_{np} \end{array}\right] = \left[\begin{array}{lll} c_{11} & \ldots & c_{1n} \\ \vdots & \ddots & \vdots \\ c_{m1} & \ldots & c_{mn} \end{array}\right], \\ c_{ij} = \sum\limits_{k=1}^n a_{ik} b_{kj}.

Умножение определено только для матриц, количество колонок первой из которых совпадает с количеством строчек второй. Умножение некоммутативно даже для квадратных матриц, и общей формулы для перестановки аргументов не существует. Умножение матриц можно рассматривать как скалярное произведение векторов-строчек первой матрицы на векторы-колонки второй матрицы. Умножение матрицы на вектор произодится по той же формуле, вторая матрица представляется как вектор-колонка.

Для матриц и векторов определены дополнительные операции.

Транспонирование матрицы или вектора-колонки, вектора-строчки:
$\left[\begin{array}{lll} a_{11} & \ldots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \ldots & a_{mn} \end{array}\right]^\text{T} = \left[\begin{array}{lll} a_{11} & \ldots & a_{1m} \\ \vdots & \ddots & \vdots \\ a_{n1} & \ldots & a_{nm} \end{array}\right].$
При транспонировании элементы меняются местами симметрично относительно главной диагонали матрицы. При транспонировании вектор-колонка превращается в вектор-строчку и наоборот. В программе транспонирование иногда реализуют как изменение схемы индексации матрицы: индекс $i$ меняется местами с индексом $j$ , однако это может снизить производительность, поскольку ячейки матрицы будут считываться программой не в том порядке, в котором они расположены в памяти.
Обращение матрицы — это вычисление обратной матрицы $A^{-1}$ , такой что $A A^{-1} = I.$ Здесь $I$ — это единичная матрица матрица, по главной диагонали которой располагаются единицы, а все остальные элементы равны нулю: $I_{ij} = \begin{cases}1, \quad i=j\\0, \quad i\neq j\end{cases}.$ Обращение матрицы используется как замена операции деления: каждый раз, когда мы хотим перенести матрицу-множитель из одной части уравнения в другую, мы домножаем обе части уравнений на обратную матрицу справа. Обратная матрица существует тогда и только тогда, когда определитель исходной матрицы не равен нулю.
Определитель матрицы: $\left|A\right| = \sum\limits_{i=1}^{n} (-1)^{i+j} a_{ij} M_{ij}.$ Здесь $M_{ij}$ — минор матрицы — определитель подматрицы, которая формируется путем удаления строчки $i$ и колонки $j$ из исходной матрицы. Определитель можно считать обобщением понятия длины вектора на матрицы. Если определитель матрицы равен нулю, то такая матрица называется вырожденной.
Длина вектора: $\left|\vec{a}\right| = \left|\vec{a}\cdot\vec{a}\right| = \sqrt{\sum\limits_{i=1}^n a_i^2}.$

В программах, как правило, вместо векторов и матриц используются многомерные массивы. Для них определены всевозможные арифметические, тригонометрические и другие операции поэлементно. Если же вам необходимо непоэлементную операцию, то для этого используются отдельные функции. Многомерные массивы ускоряют поэлементные операции за счет использования векторных регистров процессора, что является основным их назначением. Ускорение матричных и векторных операций производится за счет использования соответствующих библиотек.

Итого, векторы и матрицы — это специальная нотация для краткой записи уравнений. Для них определены все арифметические операции кроме деления: сложение и вычитание производится поэлементно, а умножение производится по специальным формулам. Также для матриц определено понятние обратной, которое используется вместо деления, понятие определителя, которое используется для проверки существования обратной матрицы и в других операциях и операция транспонирования, которая используется в матричных преобразованиях. Основное назначение матриц и векторов в численных методах — краткая запись методов решения систем уравнений.

Метод прямой и обратной подстановки

Этот метод решения систем линейных алгебраических уравнений (СЛАУ) подходит для верхних (нижних) треугольных матриц — матриц, элементы которых, стоящие ниже (выше) главной диагонали, равны нулю. Для таких матриц компоненты искомого вектора вычисляются итеративно, начиная с последней (первой) компоненты. Прямая подстановка для нижней треугольной матрицы записывается как

L x = b = \left[\begin{array}{lll} a_{11} & \ldots & 0 \\ \vdots & \ddots & \vdots \\ a_{n1} & \ldots & a_{nn} \end{array}\right] \left[\begin{array}{l} x_1 \\ \vdots \\ x_n\end{array}\right] = \left[\begin{array}{l} b_1 \\ \vdots \\ b_n\end{array}\right] \Rightarrow x_i = \frac{1}{a_{ii}} \left(b_i - \sum\limits_{j=1}^{i-1} a_{ij} x_i\right), \quad i=1,\ldots,n. \\

Обатная подстановка для верхней треугольной матрицы записывается как

U x = b = \left[\begin{array}{lll} a_{11} & \ldots & a_{1n} \\ \vdots & \ddots & \vdots \\ 0 & \ldots & a_{nn} \end{array}\right] \left[\begin{array}{l} x_1 \\ \vdots \\ x_n\end{array}\right] = \left[\begin{array}{l} b_1 \\ \vdots \\ b_n\end{array}\right] \Rightarrow x_i = \frac{1}{a_{ii}} \left(b_i - \sum\limits_{j=i+1}^{n} a_{ij} x_i\right), \quad i=n,\ldots,1. \\

Методы решения СЛАУ для матриц более общего вида строятся на преобразовании этих матриц к треугольным и применении прямой или обратной подстановки.

$LU$ -разложение

Этот метод является базовым для применения других методов и подходит для матриц общего вида. Суть метода заключается в нахождении нижней и верхней треугольных матриц, произвдение которых равно исходной матрице. Для того чтобы получить верхнюю треугольную матрицу, мы последовательно домножаем исходную матрицу на нижние треугольные матрицы особого вида. Произведение этих нижних треугольных матриц без исходной матрицы даст нам матрицу, обратной по отношению к которой является искомая нижняя треугольная матрица, а вместе с исходной даст верхнюю треугольную.

A = L_1^{-1} L_1 A = L_1^{-1} L_2^{-1} L_2 L_1 A = \ldots = \underbrace{L_1^{-1}L_2^{-1} \ldots L_{n-1}^{-1}}_{L}\, \underbrace{L_{n-1} \ldots L_2 L_1 A}_{U}, \\ L_i = \left[\begin{array}{lllll} 1 \\ & \ddots \\ & & 1 \\ & & -l_{i+1,i} & \ddots \\ & & -l_{n,i} & & 1 \\ \end{array}\right], \quad L_i^{-1} = \left[\begin{array}{lllll} 1 \\ & \ddots \\ & & 1 \\ & & l_{i+1,i} & \ddots \\ & & l_{n,i} & & 1 \\ \end{array}\right], \quad l_{i,j} = \frac{a_{ij}}{a_{jj}}.

$LU$ -разложение применяется для следующих методов.

Решение СЛАУ. Решение системы уравнений можно реализовать с помощью метода прямой и обратной подставновки.
$A x = L U x = b \Rightarrow \begin{cases} Ly = b \\ Ux = y \end{cases}.$
Вычисление обратной матрицы. Для этого мы решаем систему уравнений с несколькими правыми частями методом прямой и обратной подставновки для каждой колонки матрицы из правой части.
$A X = L U X = I \Rightarrow \begin{cases} LY = I \\ UX = Y \end{cases}.$
Вычисление определителя матрицы. Для треугольной матрицы можно легко вычислить определитель путем перемножения всех элементов главной диагонали, и он будет совпадать с определителем исходной матрицы.

$LU$ -разложение имеет более эффективные аналоги для различных типов матриц. Для симметричных положительно определенных матриц используется разложение Холецкого, для таких же, но действительных матриц, — его модификация — $LDL^T$ -разложение.

Метод Гаусса

Этот метод подходит для решения систем с матрицей общего вида. Суть метода заключается в преобразовании матрицы в верхнюю треугольную и нахождении решения методом обратной подстановки. В целом, идея этого метода аналогична расмотренному ранее $LU$ -разложению с той лишь разницей, что вычисляется только верхняя треугольная матрица, а затем выполняется только обратная подстановка. Мы рассматриваем метод Гаусса из-за его распространенности и простоты.

Разберем этот метод по шагам.

Составляем расширенную матрицу, добавляя вектор свободных членов в качестве последней колонки исходной матрицы. Это делается для удобства объяснения метода. $A x = b \Rightarrow A' = \left[\begin{array}{ccc}A & | & b\end{array}\right].$
Движемся по колонкам матрицы и для каждой колонки ищем строку матрицы с максимальным диагональным элементом этой колонки. Меняем найденную строку и строку, номер которой совпадает с номером текущей колонки. Далее, используя элементарные операции над строками матрицы (сложение, вычитание и умножение на константу), делаем так, что все элементы текущей колонки во всех строках, находящихся ниже текущей, обнуляются. Для этого домножаем текущую строку на нужный коэффициент и вычитаем ее из строки, элемент которой нужно обнулить. Также домножаем текущую строку на нужный коэффициент, так чтобы ее диагональный элемент стал равен единице. Если диагональный элемент оказывается нулем, тогда система несовместна — такая система не имеет решения. Если мысленно исключить последнюю колонку, то получается верхняя треугольная матрица, на диагонали которой стоят единицы.
Решаем получившуюся систему методом обратной подстановки.

Метод прогонки

Этот метод является более эффективным вариантом метода Гаусса для трехдиагональных матриц. Трехдиагональная матрица — это матрица, у которой все элементы кроме элементов главной диагонали и двух соседних равны нулю. Программисты называют такие матрицы ленточными, потому что в памяти удобно хранить три массива, соответствующих диагоналям, а не всю матрицу целиком.

A x = d, \quad \left[\begin{array}{llllll} b_1 & c_1 \\ a_2 & b_2 & c_2 \\ & a_3 & b_3 & c_3 \\ & & \ddots & \ddots \\ & & & a_n & b_n \end{array}\right] x = \left[\begin{array}{l} d_1 \\ d_2 \\ \vdots \\ d_n \end{array}\right].

Метод состоит из прямой и обратной прогонки.

void thomas(const float* a, const float* b, const float* c, const float* d, float* x, int n) {
  for (int i=1; i<n; ++i) {
    float w = a[i] / b[i-1];
    b[i] -= w*c[i-1];
    d[i] -= w*d[i-1];
  }
  x[n-1] = d[n-1] / b[n-1];
  for (int i=n-2; i>=0; --i) {
    x[i] = (d[i] + c[i]*x[i+1]) / b[i];
  }
}

Метод прогонки позволяет эффективно решать системы уравнений, образующиеся при решении неявных разностных уравнений, в которых на каждом шаге вместо явной формулы нужно решать СЛАУ для вычисления решения в следующий момент времени.

Уравнение теплопроводности (неявная схема)

Решим уравнение диффузии с помощью неявной схемы. В одномерном случае уравнение запишется как

T_t = \mathcal{k} T_{xx}.

Неявная схема получается, если вместо разности вперед по времени взять разность назад:

T_{i,j}-T_{i-1,j} = \mathcal{k} \frac{\Delta t}{(\Delta x)^2} (T_{i,j-1} - 2T_{i,j} + T_{i,j+1}).

Раньше значение в следующий момент времени являлось линейной комбинацией предыдущих по времени значений из окружающих узлов сетки, а теперь все наборот: линейная комбинация значений в текущий момент времени равна значению в конкретном узле сетки в предыдущий момент времени. Другими словами, значение в предыдущий момент времени равно линейной комбинации значений в следующий момент времени! Как следствие, теперь нельзя вычислять значения в каждом узле сетки параллельно, вместо этого нужно составить систему уравнений, включающую уравнения для каждого узла сетки и решить эти уравнения совместно. Чтобы это сделать, сгруппируем коэффициенты для каждого узла сетки.

-C T_{i,j-1} + (1 + 2C) T_{i,j} - C T_{i,j+1} = T_{i-1,j}, \qquad C = \mathcal{k} \frac{\Delta t}{(\Delta x)^2}.

Теперь запишем систему уравнений для граничных условий $T(t,x_\text{max}) = T(t,x_\text{min}) = 0$ :

\left[\begin{array}{rrrrr} K & -C \\ -C & K & -C \\ & \ddots & \ddots & \ddots \\ & & -C & K & -C \\ & & & -C & K \\ \end{array}\right] \left[\begin{array}{l}T_{i,2}\\T_{i,3}\\\vdots\\T_{i,N-1}\end{array}\right] = \left[\begin{array}{l}T_{i-1,2}\\T_{i-1,3}\\\vdots\\T_{i-1,N-1}\end{array}\right], \qquad K = 1 + 2C.

В этой системе в левой части находятся слагаемые для текущего момента времени, в правой части находятся слагаемые для предыдущего момента времени, а каждая строчка соответствует одному узлу сетки. Строчки, соответствующие границам, убраны из матрицы, так как содержат одни нули.

Теперь проведем анализ устойчивости по методу фон Неймана.

-A_i C \exp(i \lambda (x - \Delta x)) + A_i (1 + 2C) \exp(i \lambda x) - A_i C \exp(i \lambda (x + \Delta x)) = A_{i-1} \exp(i \lambda x)

Делим обе части уравнения на $A_{i-1}\exp(i \lambda x)$ и получаем

-\frac{A_i}{A_{i-1}} C \exp(- i \lambda \Delta x) + (1 + 2C) \frac{A_i}{A_{i-1}} - \frac{A_i}{A_{i-1}} C \exp(i \lambda \Delta x) = 1, \\ -\frac{A_i}{A_{i-1}} 2C \cos(\lambda \Delta x) + (1 + 2C) \frac{A_i}{A_{i-1}} = 1. \\

Условие устойчивости запишется как

\left|\frac{A_i}{A_{i-1}}\right| \leq 1, \\ \left|\frac{1}{-2 C \cos(\lambda \Delta x) + 1 + 2C}\right| \leq 1, \\ -1 \leq \frac{1}{-2 C \cos(\lambda \Delta x) + 1 + 2C} \leq 1, \\ \begin{cases} 1 \leq -2 C \cos(\lambda \Delta x) + 1 + 2C \\ 1 \geq -(-2 C \cos(\lambda \Delta x) + 1 + 2C) \\ \end{cases}, \begin{cases} 1 \geq \cos(\lambda \Delta x) \\ 1 + 1/C \leq \cos(\lambda \Delta x) \\ \end{cases}.

Второе неравенство никогда не выполнятся, значит наше предположение о знаке выражения под модулем было неверным, и мы можем это неравенство отбросить. Первое неравенство выполняется всегда, а это значит, что наше разностное уравнение безусловно устойчиво. Мы можем выбрать любой шаг по времени для этой системы уравнений, однако, не забывайте, что при больших шагах по времени разностное уравнение перестанет сходиться к дифференциальному!

Задания

Определитель v21 балл

Реализуйте вычисление определителя для квадратной матрицы произвольного размера. Для этого воспользуйтесь $LU$ -разложением. Проверьте себя либо с помощью детерминантов для небольших матриц, либо с помощью Wolfram Alpha.

Уравнение диффузии v32 балла

Решите одномерное уравнение диффузии с помощью неявной разностной схемы (разности назад по времени) на регулярной сетке. Систему уравнений на каждом шаге решите методом прогонки. Граничные условия следующие.

\rho(0,x) = \exp(-|x|^2), \\ \rho(t,x_\text{min}) = \rho(t,x_\text{max}).

Уравнение переноса v33 балла

Решите двухмерное уравнение переноса с помощью неявной разностной схемы (разности назад по времени) на регулярной сетке. Систему уравнений на каждом шаге решите методом прогонки/Гаусса/ $LU$ -разложения. Граничные условия следующие.

\rho(0,x) = \exp(-|x|^2-|y|^2), \\ \rho(t,x_\text{min},y) = \rho(t,x_\text{max},y), \\ \rho(t,x,y_\text{min}) = \rho(t,x,y_\text{max}).

Видео

2023

00:00 Введение.
01:11 Типы матриц.
04:10 Треугольные матрицы.
05:24 $LU$ -разложение.
11:33 Метод прогонки.
14:25 Неявная схема для уравнения диффузии.
31:20 Заключение.
32:16 Задания.

Запись лекции 05.05.2023.

2022

00:00 Введение.
00:52 Типы матриц.
04:08 Треугольные матрицы.
06:45 $LU$ -разложение.
13:35 Метод прогонки.
16:25 Неявная схема для уравнения диффузии.
27:02 Задания.

Запись лекции 05.05.2022.

Содержание

§ 12. Линейные алгебраические уравнения

Введение

Определения

Метод прямой и обратной подстановки

LULULU-разложение

Метод Гаусса

Метод прогонки

Уравнение теплопроводности (неявная схема)

Задания

Определитель v21 балл

Уравнение диффузии v32 балла

Уравнение переноса v33 балла

Видео

2023

2022

Доска

2022

$LU$ -разложение