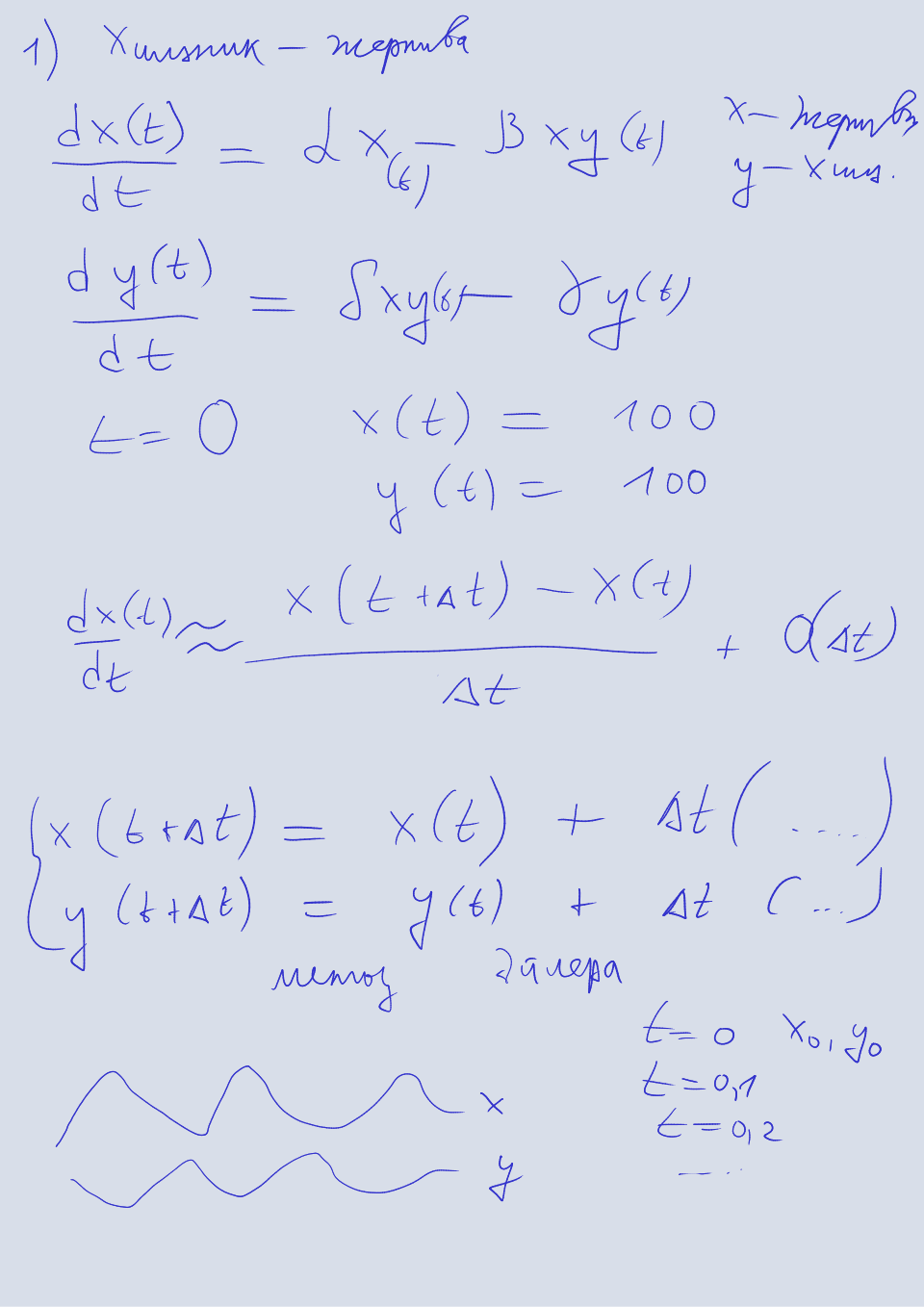§ 8. Обыкновенные дифференциальные уравнения

Математическая постановка задачи

Обыкновенными дифференциальными уравнениями (ОДУ) называются уравнения, содержащие неизвестную функцию и ее производные. В общем виде ОДУ порядка $n$ записывается как

Здесь $y=f(x)$ — неизвестная функция, вид которой требуется определить, $y^{(n)}=f^{(n)}(x)$ — ее производная по $x$ порядка $n$, а $x$ — аргумент этой функции.

Линейными ОДУ называются уравнения вида

Однородными называются линейные ОДУ, в которых правая часть равна нулю: $g(x)=0$.

Основным отличием ОДУ от алгебраических уравнений является тот факт, что решением является функция, а не конкретное число. Чтобы найти эту функцию аналитически, требуется тем или иным способом проинтегрировать уравнение по аргументу этой функции. Из-за этого процесс решения ОДУ часто называют интегрированием, а численное решение может быть получено методами численного интегрирования, которые мы рассмотрели в предыдущем разделе.

Как известно, чтобы получить конкретное значение неопределенного интеграла, нужно узнать, чему равна константа. Для того чтобы определить значение константы, используются либо граничные условия — дополнительные уравнения на границах области, в которой решается задача, либо начальные условия — значения функции в некоторой начальной точке.

Далее мы рассмотрим ОДУ, разрешимые относительно старшей производной:

Для таких уравнений доказывается существование и единственность решения. Также для них можно получить численное решение с помощью методов численного интегрирования. Теперь рассмотрим наиболее простой метод для решения такой задачи.

Метод Эйлера

Этот метод является аналогом метода прямоугольников для численного интегрирования. Будем искать решение следующего уравнения при известных начальных условиях:

Здесь $f$ — искомая функция, которая зависит от $t$, $F$ — правая часть уравнения, а $f_0$ — значение искомой функции в момент времени $t_0$. Один шаг метода Эйлера описывается как

Переписав второе уравнение, получаем $f_i' = \frac{f_{i+1}-f_i}{\Delta t}$, то есть метод Эйлера аппроксимирует производную искомой функции тангенсом угла наклона касательной к функции. Чем меньше шаг по времени, тем точнее получается аппроксимация, а при $\Delta t \rightarrow 0$ превращается в точное определение производной.

У метода есть модификации аналогичные модификациям метода прямоугольников. Например, значение искомой функции можно вычислить в середине промежутка, соответствующего одному шагу по времени:

Более общим подходом являются так называемые многошаговые методы, в которых можно указать, сколько значений функций использовать. Рассмотрим метод Адамса—Башфорта в общем виде

Здесь $n$ — количество точек, которые используются для аппроксимации производной, $b_j$ — коэффициенты. Коэффициенты вычисляются путем решения системы уравнений

Здесь $p$ — полином степени $n$ с коэффициентами $b_k$. Эта система уравнений решается аналитически и получаются следующие коэффициенты. При $n=1$ получается метод Эйлера. При $n=2$ получается

где $F_i=F(t_i,f_i)$. При $n=3$ получается

и так далее. Этот метод является аналогом формул Ньютона—Котеса для численного интегрирования. Для первых $n-1$ шагов используются методы более низких порядков: для первого шага — метод Эйлера, для второго шага — двухшаговый метод и так далее, пока не дойдем до шага $n$.

Метод Рунге—Кутта

Этот метод является наиболее распространенным методом решения ОДУ. В общем виде шаг этого метода записывается как

где

Коэффициенты $k_j$ интерпретируются как тангенс угла наклона касательной искомой функции в некоторой точке интервала. На остальные коэффициенты накладыюватся следующие ограничения.

Общего способа вычисления коэффициентов $a,b,c$ не существует, поэтому на практике используются готовые наборы этих коэффициентов, найденные различными учеными и различными способами.

• Метод Рунге—Кутта второго порядка (РК2):
  $f_{i+1} = f_i + \Delta t k_2, \\ k_1 = F(t_i,f_i), \\ k_2 = F(t_i + \frac{\Delta t}{2}, f_i + \frac{\Delta t}{2} k_1).$
• Метод Рунге—Кутта четвертого порядка (РК4):
  $f_{i+1} = f_i + \frac{\Delta t}{6} (k_1+2k_2+2k_3+k_4), \\ k_1 = F(t_i,f_i), \\ k_2 = F(t_i + \frac{\Delta t}{2}, f_i + \frac{\Delta t}{2} k_1), \\ k_3 = F(t_i + \frac{\Delta t}{2}, f_i + \frac{\Delta t}{2} k_2), \\ k_4 = F(t_i + \Delta t, f_i + k_3).$

Метод Рунге—Кутта—Фельберга

Этот метод является наиболее совершенной модификацией, поскольку содержит формулу для вычисления оптимального размера шага, а также формулу для проверки точности метода. Сокращенно метод называется РКФ45. Один шаг метода записывается как

Здесь $f_{i+1}$ является решением, вычисленным по методу РК4, а $g_{i+1}$ — по методу РК5. Это делается, для того чтобы оценить точность интегрирования с помощью метода более высокого порядка.

Шаг по времени можно выбрать автоматически по следующей формуле.

Если $\epsilon > \epsilon_\text{max}$, то текущая итерация метода повторяется для $\Delta t = \Delta t_\text{оптимальный}$, в противном случае следующая итерация выполняется с шагом $\Delta t_\text{оптимальный}$.

Формула работает следующим образом. Текущая итерация метода повторяется до тех пор, пока погрешность не станет меньше максимально допустимой. При этом на каждой попытке шаг уменьшается пропорционально корню пятой степени от отношения максимально допустимой погрешности к текущей. Например, если погрешность превышает допустимую в два раза, то шаг уменьшается примерно на 20%. Если же погрешность становится меньше допустимой, то формула увеличивает размер шага. Например, если погрешность меньше допустимой в два раза, то шаг увеличивается примерно на 3%. Если погрешности равны, то шаг уменьшается на 10%.

Очевидно, формула носит эмпирический характер, и может быть заменена на альтернативную, исходя из особенностей задачи. Например, на формулу, которая увеличивает размер шага быстрее, если погрешность становится ниже допустимой, или на формулу, которая использует метод оптимизации для вычисления оптимального размера шага. Аналогичные формулы можно использовать и в других методах решения ОДУ.

Неявные методы

Все рассмотренные ранее методы являются явными: в формуле для текущего шага метода слева от знака равенства стоит значение функции на текущем шаге, которое мы хотим определить, а справа от знака равенства стоят значения функции на предыдущих шагах. Если же справа от знака равно поставить значение функции на текущем шаге, то метод становится неявным.

Преимущество неявных методов заключается в том, что они более устойчивы: погрешность метода и компьютерная погрешность не могут привести к расхождению (выходу на бесконечность) решения. Обычно, такое поведение присуще жестким уравнениям — уравнениям, в которых небольшие изменения значения аргумента влекут за собой большие изменения значения функции. Для каждого метода можно определить область сходимости, однако, это выходит за рамки данного курса. На практике можно воспользоваться простым правилом: если решение расходится даже при очень маленьких значениях шага, нужно попробовать неявный метод, или искать ошибку в коде.

Недостаток неявных методов заключается в том, что на каждом шаге для определения текущего значения функции необходимо в общем случае решить систему нелинейных уравнений одним из методов оптимизации, что увеличивает потребление ресурсов компьютера. В случае линейных ОДУ система уравнений также будет линейной, и она решается соответствующими методами линейной алгебры, которые будут рассмотрены в последующих разделах. В случае нелинейных ОДУ система решается методами оптимизации, которые также являются методами нахождения корня уравнения (метод бисекции, метод Ньютона и другие).

Неявный метод Эйлера записывается как

В неявных метода Рунге—Кутта коэффициенты $a_{n,j}$ определены не только для $j<n$, но и для $j=n$. Как мы уже говорили ранее, единого способа определения значений коэффициентов не существует, поэтому проще всего взять готовые неявные варианты метода.

🌊🌊🌊

Во всех методах этого раздела шаг по времени является основным фактором, влияющим на точность: даже метод Эйлера может дать более точное решение, чем метод Рунге—Кутта, если во много раз уменьшить шаг.

Обыкновенные дифференциальные уравнения являются частным случаем уравнений в частных производных, когда искомая функции зависит только от одного аргумента.

Задания

Уравнение хищник-жертва1 балл

Решите явным методом Эйлера систему уравнений хищник-жертва. Подберите максимальный шаг, при котором решение не расходится. Система имеет вид

Здесь $x(t)$ — количество жертв, $y(t)$ — количество хищников, $\alpha$ — коэффициент естественного роста популяции жертв, $\beta$ — коэффициент убыли популяции жертв из-за хищников, $\delta$ — коэффициент роста популяции хищников, $\gamma$ — коэффициент естественной убыли популяции хищников. Начальные значения $x$ и $y$ произвольные.

Уравнение второго порядка2 балла

Решите явным методом Эйлера уравнение второго порядка. Подберите шаг, при котором решение не расходится. Уравнение имеет вид

Значение функции $f$ при $t=0$ произвольное.

Уравнение движения3 балла

Решите явным методом РКФ45 уравнение поступательного движения. Уравнение имеет вид

Здесь $\vec{x}$ — координата тела, $\vec\upsilon$ — вектор скорости, $\vec{F}$ — вектор внешних сил. Начальные значения координаты и скорости произвольны. В качестве внешних сил можно взять силу тяжести $\vec{F} = m\vec{g}$, где $\vec{g} = (0,0,-g)$ — ускорение свободного падения.

Видео

2023

2022

Доска

2023

2022