§ 14. Параллельные вычисления + численные методы = ♥️

Введение

Параллельные вычисления — это вычисления, которые выполняются одновременно. Технически одновременное выполнение достигается за счет ядер или потоков процессора, узлов кластера, видеокарт и т.п. Алгоритмически одновременное выполнение достигается путем разбиения задачи на подзадачи, которые можно решать параллельно.

Наиболее важной характеристикой параллельного программы является ее ускорение — во сколько раз программа стала выполняться быстрее по сравнению с последовательной версией на конкретном числе потоков, ядер, узлов кластера и т.п. Аналогичной характеристикой параллельного алгоритма является степень параллелизма — на сколько независимых частей удалось разбить задачу.

Ускорение параллельной версии программы по сравнению с последовательной версией описывается законом Амдаля.

Здесь $t_1$ — время работы последовательной программы на одном процессоре, $t_n$ — время работы параллельной программы на $n$ процессорах, $\alpha$ — доля программы, которую удалось выполнить параллельно на $n$ процессорах. Возьмем для примера сто процессоров, тогда при $\alpha=1$ мы получим идеальное ускорение в сто раз, а уже при $\alpha=0.99$ мы получим ускорение лишь в пятьдесят раз! Однако, не стоит расстраиваться и думать, что параллельные вычисление бесполезны. Дело в том, что здесь мы имеем дело с дробью, а дробям свойственно резко менять значения (вспомните, насколько точно программы показывают скорость скачивания и копирования файлов). Согласно статье Адмаля, где он вывел этот закон, в реальных задачах производительность близка к 50% от пиковой (ускорение в $n/2$ раз вместо $n$). Согласно результатам тестов производительности LINPACK и HPCG наиболее оптимизированные задачи достигают значения 80-90% от пиковой, а задачи с очень сложным шаблоном доступа к памяти и сложным взаимодействием процессов 10-20% от пиковой. В среднем как раз получается 50%.

Почему же так происходит? Это проще всего объяснить, обратившись к похожему закону, который был выведен Бруксом эмпирическим путем и описан в книге Мифический человеко-месяц. В этой книге автор описывает свой опыт руководства командой программистов и выводит закон, который гласит, что при добавлении в команду программистов скорость разработки повышается до некоторого оптимального количества программистов, а затем начинает снижаться. То есть существует некоторое оптимальное количество программистов, которые способны выполнить проект максимально быстро. Автор объясняет этот феномен тем, что программисты в рамках своей работы взаимодействуют друг с другом, и чем больше программистов, тем больше времени им надо тратить на это взаимодействие. Когда количество программистов становится критическим, время затрачиваемое на взаимодействие, начинает превышать время, затрачиваемое на остальную работу, и производительность команды падает.

В случае закона Амдаля объяснение аналогичное: чем больше параллельных процессов используется для вычислений, тем больше времени тратится на синхронизацию работы этих процессов. Конечно, точка максимума производительности находится гораздо дальше от начала координат, нежели в случае с программистами, а снижение производительности при увеличении количества процессов можно наблюдать только в крайних случаях: обычно, после достижения оптимального числа процессов производительности начинает колебаться вокруг этого оптимального значения. Тем не менее, закон Амдаля имеет важное теоретическое значение, а также вместе с законом Брукса дает понять, что то, как решают задачи машины, очень похож на то, как эти же задачи решают люди.

Модели параллельных вычислений

Итак, мы узнали, что параллельные вычисления — это решение задачи командой процессов. Далее мы будем использовать термины поток, процесс, ядро, узел кластера свободно, имея ввиду некоторый элемент, который связан с независимой частью решаемой задачи. На данный момент существует несколько моделей, которые позволяют описать решение задачи параллельно.

Наиболее старой моделью является модель взаимодействующих последовательных процессов, разработанная Чарьзом Харом. В рамках этой модели параллельные вычисления описываются набором процессов, каждый из которых действует независимо, а для синхронизации эти процессы отправляют друг другу сообщения по каналам. Эта модель отличается простотой и практически полным соответствием тому, как реализованы процессы и их взаимодействие в операционных системах. Недостатком модели можно считать отсутствие какого-либо порядка во взаимодействии процессов: когда можно передать сообщение от любого процесса любому другому, то невозможно сделать какие-либо выводы относительно эффективности этого взаимодействия и эффективности работы всей системы в целом. На данный момент программными реализациями этой модели можно считать процессы в операционных системах, а также библиотеку MPI, которая является стандартом де факто в суперкомпьютерных вычислениях.

Более приближенной к реальности является модель BSP, которая описывает решение задачи параллельными процессами как набор последовательных супершагов. Каждый такой шаг внутри себя содержит два этапа: этап параллельного решения задачи и этап синхронизации процессов и обмена данными между ними. Эта модель более точно описывает задачи, решаемые на суперкомпьютерах — задачи, которые считывают входные данные, выполняют вычисления, записывают результат на диск и завершаются. Такие задачи называются задачи пакетной обработки (batch processing), и они действительно имеют структуру, описываемую этой моделью. На основе времени выполнения супершага, который часто является одной итерацией основного цикла программы, можно оценить, сколько времени осталось работать программе до завершения. После каждого супершага можно записать промежуточные данные на диск, чтобы потом иметь возможность начать вычисления с этого шага, а не с самого начала. Программные реализации данной модели не распространены из-за популярности MPI, наиболее близкой по структуре технологией является OpenCL, а также многие технологии анализа больших данных.

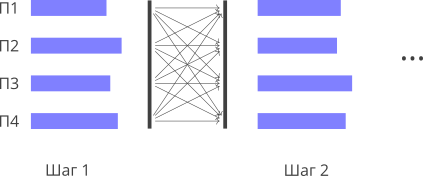
Еще одной моделью, которая описывает параллельные вычисления, является модель акторов. Эта модель больше подходит для описания задач, в которых вычисления происходят при возникновении некоторого события (как в веб-серверах). В рамках этой модели вычисления реализуются внутри методов специальных объектов, называемых акторами. Эти объекты могут отправлять друг другу сообщений, а в ответ на сообщение они могут создавать новых акторов или выполнять вычисления. Обмен сообщениями организован асинхронно через очередь. Таким образом, эта модель уходит от трудноформализуемого понятия процесса и заменяет его привычным многим программистам понятием объекта, а глобальную синхронизацию процессов, присущую модели BSP, — на асинхронное взаимодействие путем передачи сообщений. Недостатком модели можно считать более сложное взаимодействие объектов друг с другом: в этой модели оно полностью асинхронно, а один параллельный процесс может содержать в себе произвольное количество объектов. Прогаммные реализации данной модели существуют в разных языках программирования, например, в библиотеке Akka языка Scala.

Библиотеки для параллельных вычислений

Эти библиотеки реализуют ту или иную модель вычислений, а иногда несколько моделей. Библиотека может использовать одну машину или целый кластер для вычислений, а также графически и иные ускорители, установленные на узлах кластера.

Наиболее простой библиотекой является программная реализация стандарта OpenMP. Эта библиотека встраивается в компилятор разработчиками этого компилятора, после чего в программу можно добавить специальные директивы, которые запустят параллельные процессы, и, например, выполнят итерации цикла параллельно. OpenMP работает только на одном узле кластера, но последние версии позволяют использовать графические и иные ускорители для параллельных вычислений. Главным преимуществом этого стандарта является его неивазивность: параллельный код — это последовательный код с директивами, которые можно отключить во время компиляции. Как правило, для класса-солвера не нужно делать отдельную последовательную и параллельную версию: достаточно добавить в последовательную версию директивы и пересобрать код.

Библиотекой, которая повсеместно используется на суперкомпьютерах, является MPI. В это библиотеки ваша программа сразу запускается в параллельных процессах: то есть ваша программа по умолчанию выполняется параллельно, а вам лишь необходимо осуществить взаимодействие этих процессов. Взаимодействие осуществляется путем передачи сообщений от одного параллельного процесса другому. В зависимости от расположения процессов (на одной и той же машине или на разных узлах кластера) выбирается наиболее оптимальный способ передачи: если процессы расположены на одной машине, то передача осуществляется через общую память. Основным недостатком данной библиотеки является тот факт, что число процессов жестко привязано к степени параллелизма задачи и к суммарному количеству ядера процессора на узле. Получается, что если степень параллелизма задачи определяется входными данными (например, количество уравнений в системе), то вам придется найти кластер, на котором есть ровно столько свободных ядер, сколько требует задача. Конечно, вы можете запустить больше процессов, чем ядер на узле, но тогда вы столнетесь с высокими накладными расходами. Обходным решением данной проблемы является реализация динамического распределения нагрузки поверх библиотеки MPI: асинхронной рассылки сообщений всем процессам от главного процесса, в этих сообщениях описывается задача, которую нужно решить дочернему процессу. Другими словами, MPI — это скорее библиотека передачи сообщений, нежели библиотека для параллельных вычислений.

Наконец, для вычисления на видеокарте нам нужна библиотека OpenCL или CUDA. Обе эти библиотеки имеют похожую структуру: у них есть очередь команд, в которую мы асинхронно добавляем команды, а видеокарта их выполняет по порядку. Команда может быть любой: копирование данных из памяти процессора в память видеокарты и наоборот, запуск вычислений на видеокарте, синхронизация процессора и видеокарты и др. Главным недостатком этих библиотек является тот факт, что для каждого класса-солвера необходимо создать отдельный подкласс, который реализует вычисления на видеокарте. Это фактически удваивает усилия программиста: сначал он или она пишет код для процессора, проверяет его корректность с помощью тестов, затем пишет код для видеокарты и проверяет его корректность. Если же потом код нужно будет модифицировать, добавив какие-то улучшения, то модифицировать придется оба варианта кода, иначе они перестанут выдавать один и тот же результат. Получается, видеокарты ускоряют вычисления за счет замедления скорости разработки программы, что оправдано только если ускорение значительное, а во всех других случаях наличие большого количества процессорных ядер, использующих ту же самую память, что и процессор, позволило бы повысить производительность без значительных усилий. Хочется верить, что такие процессоры появятся в скором будущем в открытом доступе, а не только в суперкомпьютерах.

Векторизация

Помимо параллельных вычислений в нескольких процессах или потоках, для повышения производительности используют параллельные вычисления, реализуемые за счет векторных регистров процессора. Векторные регистры представляют собой расширение обычных скалярных регистров для целых чисел и чисел с плавающей точкой. При наличии векторных регистров в дополнение к каждому скалярному регистру ставится еще несколько таких же, которые образуют вектор (массив). Когда процессор производит поэлементные операции с этими регистрами, они одновременно производятся со всеми регистрами из вектора, что приводит к повышению производительности. Также существуют специальные операции, которые производятся с вектором целиком: перестановка элементов, сдвиги и др.

Как же использовать эти операции у себя в программе? Самый простой и надежный способ — использовать библиотеки многомерных массивов, в которых эти операции реализованы с помощью ассемблерных вставок. Это гарантирует, что на любом процессоре, который поддерживается такой библиотекой, операции над массивами будут работать с максимальной производительностью. Второй способ — помочь компилятору автоматически векторизовать код. Для этого нужно переписать цикл так, чтобы на одной итерации использовался только один элемент каждого из массивов, используемых в цикле. Тогда компилятор обнаружит поэлементную обработку и заменит скалярные операции на их векторные аналоги. Гарантировать это невозможно, потому что на это влияет множество факторов: компилятор, процессор, флаги компиляции, а также сложность цикла и используемые операции. Тем не менее, оптимизированные под векторные операции циклы повышают качество кода и не снижают портируемость программы на новые процессоры. Наконец, третий способ — сделать ассемблерные вставки самостоятельно. Это даст максимальный контроль за производительностью, но программа будет работать только на процессорах, на которых есть соответствующие инструкции. Чтобы расширить список процессоров, на которых работает программа, используют так называемую динамическую диспетчеризацию — выбор ветки кода с нужными инструкциями во время работы программы в зависимости от процессора. Это реализуется с помощью инструкции CPUID.

Примеры нетривиальных параллельных алгоритмов

Во многих случаях параллелизм программы сводится к параллельному выполнению независимых друг от друга итераций цикла программы, и в таких случаях параллелизм реализуется тривиально. Чтобы окунуться в мир параллельных вычислений, интереснее всего рассмотреть алгоритмы, в которых параллелизм не так просто извлечь. Сейчас мы рассмотрим некоторые из них.

Вихрь Мерсенна

Этот алгоритм используется для генерации псевдослучайных чисел. На данный момент он является наиболее часто используемым из-за высокого качества генерируемых последовательностей, а также из-за астрономического периода $2^{19937}-1$. Этот алгоритм, как и многие его аналоги, является последовательным. Как же нам сделать так, чтобы мы могли генерировать параллельно несколько последовательностей псевдослучайных чисел?

Конечно, мы можем это сделать, создав несколько генераторов и инициализировав их различными начальными значениями. Однако, этот подход имеет свои подводные камни. Дело в том, что нет гарантии, что последовательности чисел, генерируемые параллельно, не будут коррелированы друг с другом. Это может привести к аномалиям при анализе вывода программы, который использовал эти последовательности (например поле векторов скорости ветра и т.п.). В случае Вихря Мерсенна существует специальный метод, который решает эту проблему.

Для того чтобы последовательности генераторов не был коррелированы друг с другом, их параметры необходимо сгенерировать с помощью дополнительного генератора. Этот метод именуется динамическим созданием Вихрей Мерсенна. Генерация параметров для большого количества потоков (генераторов) — это долгий процесс, но его можно выполнить один раз заранее для заведомо большого числа генераторов и сохранить параметры в файл. Затем в основной программе этот файл считывается, и параметры из него используются для создания генератора для каждого параллельного потока. Затем эти генераторы используются, как обычно, но период каждого генератора теперь делится на количество генераторов в файле.

Модель авторегрессии

Эта статистическая модель используется для анализа и прогнозирования временных рядов. Наиболее популярна ее одномерная версия, однако двухмерные и трехмерные версии также используются, например, для анализа изображений. Суть модели заключается в предположении, что значение функции в каждой точке равно взвешенной сумме предыдущих по времени и пространству точек плюс некоторый белый шум. В трехмерном случае это записывается как

Здесь $\zeta$— это исследуемая функция, значения которой мы прогнозируем (генерируем), $\Phi$ — это коэффициенты авторегресии, $\epsilon$ — белый шум. За границами массива функция равна нулю.

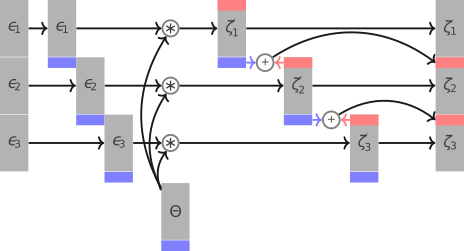
Наша задача заключается в том, чтобы сгенерировать значения функции по известным значениям белого шума и коэффициентов. Несложно заметить, что между точками, в которых мы генерируем значения функции, существуют информационные зависимости: для того чтобы сгенерировать значение в точке $(1,1,1)$, необходимо сначала сгенерировать значения в семи предыдущих точках $(0,0,0), (0,0,1), (0,1,0), (1,0,0), (1,1,0), (0,1,1), (1,0,1)$. Для того чтобы реализовать параллельную генерацию, существует два способа.

Первый способ заключается в том, чтобы генеирировать параллельно точки, находящиеся на диагонали (в двухмерном случае) или в одной диагональной плоскости (в трехмерном случае). Для этого нужно запустить последовательный цикл по диагоналям, а внутри — параллельный цикл по всем точкам, и генерировать только те, сумма индексов которых равна номеру диагонали. Этот алгоритм прост, но неэффективен, поскольку содержит в себе глобальную синхронизацию потоков после генерации каждой диагонали.

Альтернативный способ заключается в том, чтобы разбить массив на блоки одинакового размера (но не меньше количества коэффициентов по каждому из измерений) и сформировать из них очередь задач. Затем каждый параллельный поток сканирует очередь в поисках блока, для которого сгенерированы все предыдущие блоки, извлекает этот блок, генерирует в нем точки и помечает, как готовый. Извлечение повторяет до тех пор, пока очередь не опустошится. Этот алгоритм уже не содержит глобальной синхронизации длиной в целую итерацию, однако при извлечении блока из очереди все равно придется синхронизировать потоки. Также здесь можно регулировать степень параллелизма путем изменения размера блока.

Модель скользящего среднего

Эта модель также используется для анализа и прогнозирования временных рядов наравне с авторегресиионной моделью. Ее формула похожа, но не содержит информационных зависимостей.

Здесь $\zeta$— это исследуемая функция, значения которой мы прогнозируем, $\Theta$ — это коэффициенты скользящего среднего, $\epsilon$ — белый шум. За границами массива белый шум равен нулю.

Наша задача опять заключается в параллельной генерации значений функции по известным значениям коэффициентов и белого шума. Существует по крайней мере два способа это сделать.

Первый способ заключается в параллельном попарном суммировании. Этот способ прост в реализации, однако не дает максимальной производительности.

Второй способ заключается в использовании быстрого преобразования Фурье. Дело в том что формула является сверткой коэффициентов и белого шума. По теореме о свертке ее можно записать с помощью преобразований Фурье.

Здесь мы можем вычислить каждое из преобразований Фурье параллельно, но это опять неэффективно, поскольку массив коэффициентов и массив белого шума имеют разные размеры, а это означает, что нам придется их приводить к одному размеру с помощью интерполяции. Решением данной проблемы является параллельный алгоритм свертки.

Алгоритм следующий. Мы делим массив белого шума, размер которого больше, на равные части, размер которых совпадает с размером массива коэффициентов, и перед началом каждой части и перед началом массива коэффициентов дописываем некоторое количество нулей. Затем мы параллельно производим свертку каждой части с массиво коэффициентов, а затем параллельно суммируем друг с другом точки, находящиеся на пересечении смежных частей. Получается финальный массив, в котором хранится результат свертки. Индивидуальный свертки, которые мы делаем в каждом потоке, при этом реализуются с помощью последовательных быстрых преобразований Фурье.

Этот алгоритм отличается большим количеством вложенного параллелизма: параллелизм по частям массива белого шума, два преобразования Фурье из трех можно вычислить параллельно, каждое из преобразований Фурье также можно реализовать параллельно внутри, и суммирование смежных частей также можно делать параллельно. Такие алгоритмы идеальны для видеокарт, в архитектуре которых содержится много вложенного параллелизма, а также преобразование Фурье реализовано на видеокартах с очень высокой эффективностью.

🌊🌊🌊

В этом лекции мы познакомились с параллельными вычислениями. Эти вычисления используются для повышения производительности программ за счет использования нескольких потоков или ядер процессора, нескольких процессоров, нескольких узлов кластера, графических ускорителей, а также векторных регистров процессора. Особенностью данных вычислений является сложность их формализации и программирования: порой простые с точки зрения математики формулы и модели переносятся на параллельные вычисления нетривиальным образом. Эти вычисления используются, в основном, на суперкомпьютерах для решения прикладных научных задач, но также в индустрии для анализа больших объемов данных. В условиях, когда частоту процессора больше не удается повысить параллельные вычисления являются единственным способом повышения производительности программ, значит сфера их применения будет расширяться.

Задания

Параллельный Вихрь Мерсенна1 балл

Сравните коррелированность последовательностей псевдослучайных чисел, сгенерированных двумя способами.

1. Два генератора, отличающихся только полем seed, которое определяется как текущее время в наносекундах.
2. Два генератора, созданных с помощью библиотеки DCMT, которые отличаются настройками, а поле seed у них одинаковое и равно текущему времени в наносекундах.

где $\mu$ — среднее значение выборки, $s$ — среднеквадратичное отклонение, $n$ — размер выборки.

#include <cstdint>
#include <limits>
#include <iterator>
#include <algorithm>
#include <cstring>

extern "C" {
#include "dc.h"
}

struct mt_config: public ::mt_struct {

    inline mt_config() { std::memset(this, 0, sizeof(mt_config)); }
    inline ~mt_config() { free(this->state); }
    inline mt_config(const mt_config& rhs) { std::memset(this, 0, sizeof(mt_config)); this->operator=(rhs);
    }

    mt_config& operator=(const mt_config& rhs) {
        free_state();
        std::memcpy(this, &rhs, sizeof(mt_config));
        init_state();
        std::copy_n(rhs.state, rhs.nn, this->state);
        return *this;
    }

private:

    inline void init_state() { this->state = (uint32_t*)malloc(this->nn*sizeof(uint32_t)); }
    inline void free_state() { if (this->state) { free(this->state); } }

    friend std::istream&
    operator>>(std::istream& in, mt_config& rhs) {
        rhs.free_state();
        in.read((char*)&rhs, sizeof(mt_config));
        rhs.init_state();
        in.read((char*)rhs.state, rhs.nn*sizeof(uint32_t));
        return in;
    }

    friend std::ostream&
    operator<<(std::ostream& out, const mt_config& rhs) {
        out.write((char*)&rhs, sizeof(mt_config));
        out.write((char*)rhs.state, rhs.nn*sizeof(uint32_t));
        return out;
    }

};

template<int p=521>
struct parallel_mt_seq {

    typedef mt_config result_type;

    inline explicit parallel_mt_seq(uint32_t seed): _seed(seed) {}
    inline result_type operator()() { this->generate_mt_struct(); return _result; }

    template <class OutputIterator>
    void param(OutputIterator dest) const {
        *dest = _seed; ++dest;
    }

private:

    void
    generate_mt_struct() {
        mt_config* ptr = static_cast<mt_config*>(::get_mt_parameter_id_st(nbits, p, _id, _seed));
        if (!ptr) {
            throw std::runtime_error("bad MT");
        }
        _result = *ptr;
        ::free_mt_struct(ptr);
        ++_id;
    }

    uint32_t _seed = 0;
    uint16_t _id = 0;
    result_type _result;

    static const int nbits = 32;

};

struct parallel_mt {

    typedef uint32_t result_type;

    inline explicit parallel_mt(mt_config conf): _config(conf) { init(0); }
    inline result_type operator()() noexcept { return ::genrand_mt(&_config); }
    inline result_type min() const noexcept { return std::numeric_limits<result_type>::min(); }
    inline result_type max() const noexcept { return std::numeric_limits<result_type>::max(); }
    inline void seed(result_type rhs) noexcept { init(rhs); }

private:

    inline void init(result_type seed) { ::sgenrand_mt(seed, &_config); }

    mt_config _config;

};

Параллельная авторегрессия2 балла

Реализуйте в существующей программе параллельную версию трехмерной модели авторегрессии вторым способом, описанном в конспекте (через очередь блоков). В репозитории есть последовательная версия программы, использующей эту модель.

git clone https://courses.igankevich.com/numerical-methods/autoreg.git
cd autoreg         # переходим в директорию с исходным кодом
make               # собираем основную программу
./autoreg          # запускаем основную программу
ls -l zeta         # при успешном выполнении должен появиться файл zeta в текущей директории
make visual        # собираем программу для визуализации
./visual zeta      # запускаем визуализацию

Параллельная свертка3 балла

Напишите программу, в которой реализована параллельная свертка по алгоритму с суммирование накладывающихся частей и без преобразования Фурье. Проверьте себя с помощью последовательной версии.

Видео

2022