§ 11. Дифференциальные уравнения в частных производных на нерегулярных сетках

Введение

В предыдущем разделе мы рассмотрели методы решения ДУЧП, основанные на вычислении конечных разностей в узлах регулярной сетки, однако в реальных задачах сетка, как правило, нерегулярная треугольная, то есть состоит из тетраэдров. Также конечные разности значений функции в узлах сетки не позволяют закодировать законы сохранения в разностном уравнении. Для того чтобы решить эти проблемы, были придуманы методы конечных объемов, которые являются обобщением методов конечных разностей на треугольную нерегулярную сетку и в которых обеспечивается соблюдение законов сохранения.

Метод конечных объемов

Этот метод основан на применении теоремы Остроградского—Гаусса к ячейкам (конечным объемам), на которые мы разделили область, в которой мы решаем дифферециальное уравнение. Ячейками называют пространство между узлами сетки: в одномерном случае это просто отрезок, в трехмерной нерегулярной треугольной сетке это тетраэдр. Ячейки могут иметь любую удобную для вычислений форму.

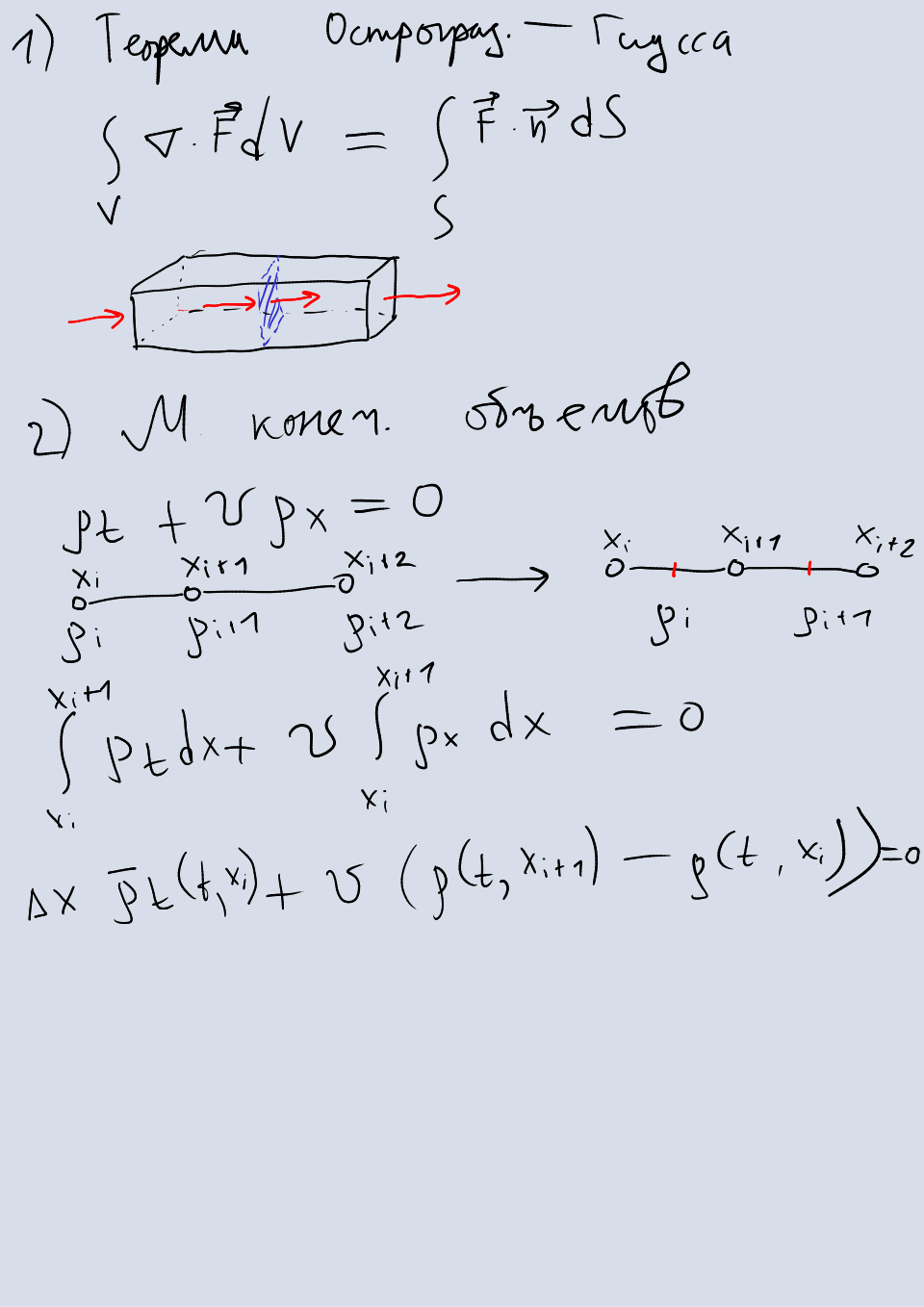
Теорема Остроградского—Гаусса гласит, что градиент плотности (или любой другого свойства субстанции, записываемого в виде вектора) в замкнутом объеме может происходить только путем перемещения субстанции внутрь и наружу этого объема. Математически это записывается как равенство интеграла дивергенции градиента плотности по объему интегралу градиента плотности по площади границы этого объема.

Это равенство можно объяснить слеюдущим образом. Если мы разделим конечный объем на объемы меньшего размера (тетраэдры), которые соприкасаются друг с другом, то изменение градиента плотности равно массе, вышедшей или вошедшей через каждую грань тетраэдра. Однако, на соприкасающихся гранях эти массы равны, а значит, единственные грани, через которые входит и выходит масса, — это внешние грани тетраэдров, находящихся на границе исходного конечного объема. Другими словами, изменение массы внутри конечного объема равно разности вошедшей и вышедшей за границы этого объема массы.

Уравнение переноса

Применим метод конечных объемов для решения одномерного уравнения переноса.

В одномерном случае вместо объемов — отрезки, а вместо граней — точки начала и конца этих отрезков. Чтобы применить метод конечных объемов, проинтегрируем обе части уравнения по объему.

Теперь заменим интеграл по объему на интеграл по площади, используя теорему Остроградского—Гаусса. В одномерном случае это просто разница значений плотности на левой и правой границе отрезка.

Нам осталось избавиться от интеграла в левой части. Для этого воспользуемся теоремой о среднем: заменим интеграл на среднее значение плотности, домноженное на разницу пределов интегрирования.

Если заменить производную по времени конечной разностью, то получится то же самое разностное уравнение, что и в предыдущем разделе, однако плотность вычисляется в середине отрезка, а не на границах. Несмотря на это, значения на границах нам все равно нужны для вычисления значения в середине. Значения на границах обычно получают с помощью интерполяции.

Теперь перепишем последнюю формулу для трехмерного пространства и сетки из тетраэдров.

Здесь $i$ обозначает номер грани тетраэдра, $\vec{n}_i$ — нормаль к этой грани, $S_i$ — площадь грани, а $\rho(t,\vec{x}_i)$ — значение плотности в центре грани. Плотность в центре также вычисляется путем интерполяции.

Уравнение диффузии

Применим метод конечных объемов для решения одномерного уравнения диффузии

Произведем те же самые преобразования, что и для уравнения переноса.

Если заменить оставшиеся производные на конечные разности, то получится такое же разностное уравнение, что и в предыдущем разделе, но плотность вычисляется в центре отрезка. Запишем ту же самую формулу для тетраэдра.

Заключение

Метод конечных объемов позволяет обобщить методы конечных разностей на нерегулярные треугольные сетки. Его премуществом является автоматическое соблюдение законов сохранения, поскольку он основан на этих законах. Несмотря на это, получившееся разностное уравнение также нужно проверять на устойчивость и сходимость, как и в случае метода конечных разностей. Здесь мы этого не делали, чтобы не повторяться.

Задания

Уравнение переноса v21 балл

Решите уравнение переноса в одномерном случае с помощью метода конечных объемов. В качестве сетки используйте отрезки произвольной длины. Не забудьте про условие устойчивости при выборе шага по времени. Начальные и граничные условия следующие.

Уравнение диффузии v22 балла

Решите уравнение диффузии в двухмерном случае с помощью метода конечных объемов. В качестве сетки используйте прямоугольники с произвольной длиной сторон: длина прямоугольников по $x$ в одной колонке совпадает, длина прямоугольников по $y$ в одной строчке также совпадает. Не забудьте про условие устойчивости при выборе шага по времени. Начальные и граничные условия следующие.

Уравнение переноса-диффузии v23 балла

Решите уравнение переноса-диффузии (сумма уравнение переноса и диффузии) в тремерном случае на нерегулярной треугольной сетке с помощью метода конечных объемов. В качестве сетки используйте цилиндр. Не забудьте про условие устойчивости при выборе шага по времени. Начальные и граничные условия следующие.

Граничное условие означает, что обмен массой через границы цилиндра не происходит.

Видео

2023

2022

Доска

2023

2022