§ 10. Дифференциальные уравнения в частных производных на регулярных сетках

Введение

Эти уравнения являются обобщением ОДУ на многомерное пространство: в уравнении присутствуют производные сразу по нескольким аргументам функции. Методы, предназначенные для решения ОДУ, здесь не применимы, поскольку интегрировать уравнение нужно сразу по нескольких аргументам, а из получившегося уравнения выразить решение в явном виде не представляется возможным. Тем не менее, для ДУЧП были разработаны свои численные методы решения, которые коллективно называются разностные схемы.

Разностная схема это запись ДУЧП, в которой все производные заменены на их разностные аналоги, которые мы изучили в предыдущем разделе. За кажущейся простотой скрывается нетривиальное требование сходимости разностной схемы к точному решению уравнения при стремлении размера сетки к нулю. Часто можно лишь проверить готовую схему на сходимость, а составить схему так, чтобы она заведомо сходилась, можно лишь эмпирическим путем. Также для различных уравнений подходят различные схемы; можно без большого преувеличения сказать, что схемы уникальны для каждого уравнения.

Уравнение диффузии

Рассмотрим, как строится разностная схема на примере уравнения диффузии (теплопроводности).

Здесь $T$ — это температура некоторого объекта, а $\mathcal{k}$ — коэффициент температуропроводности этого объекта. В одномерном случае уравнение принимает вид

Теперь запишем все производные этого уравнения с помощью конечных разностей. Для производной по времени будем использовать разность вперед первого порядка точности, а для пространственной производной — центральную разность второго порядка точности.

Сокращенно это можно записать как

Теперь проверим устойчивость схемы методом фон Неймана. Для того чтобы разностная схема была устойчива, необходимо, чтобы абсолютное значение отношения амплитуды решения убывало со временем:

Для того чтобы вычислить амплитуду решения, представим его в виде ряда Фурье. Ряд Фурье — это представление функции в виде суммы гармоник различных фаз и амплитуд.

Подставим это выражение в разностную схему и уберем знак суммы, поскольку это линейное уравнение.

Делим обе части уравнения на $A_{i}\exp(i \lambda x)$ и получаем

Упрощаем уравнение, используя тригонометрические равенства.

Для того чтобы разностная схема была устойчива, должно быть выполнено условие

Неравенство $G \leq 1$ выполняется всегда, а неравенство $G \geq -1$ выполняется, когда

Итого, мы выяснили, что разностная схема устойчива, если шаг по времени много меньше шага по пространству. Это условие можно легко запрограммировать, чтобы запретить запуск программы с шагами по времени и пространству, которые этому условию не удовлетворяют.

Мы составили для ДУЧП разностную схему, но для решения реальной задачи распространения тепла в некотором объекте, у нас не хватает начальных и граничных условий. Под начальными условиями понимается некоторое исходное состояние системы. В нашем случае это температура в каждой точке сетки. Это распределение может быть любым, и за продолжительное время температура должна стать одинаковой в каждой точке. Например, можно взять начальное распределение

Граничными условиями называются дополнительные условия в конкретных областях сетки (как правило, на границах). Эти условия необязательны для этой задачи. Если их нет, то нам надо как-то вычислить производную по пространству на границе сетки. Как правило, на границе вместо центральной разности используется разность вперед или назад, однако использование центральной разности в тестовых целях также допускается: при этом надо обнулить все точки, которые выходят за границу. В окончательных версиях программ, конечно, используют разности вперед и назад.

Отличие разностных схем от дифференциальных уравнений

В рассмотренном ранее ДУЧП все производные были заменены на их разностные аналоги, другими словамия, все бесконечно малые были заменены на конечные величины. Влияние такой замены можно описать математически. Для этого разложим в ряд Тейлора $T_{i+1,j},T_{i,j-1},T_{i,j+1}$ в окрестности точки, которая соответствует индексам $(i,j)$, и получим

Теперь подставим получившиеся выражения в разностную схему и получим

Преобразуя, получаем исходное уравнение с дополнительным слагаемым в правой части:

Это и есть дифференциальное уравнение, точное решение которого совпадает с точным решением разностного уравнения. В данном уравнении появилось дополнительное слагаемое, однако, оно стремится к нулю при шаге по времени, стремящемся к нулю. В других уравнениях могут появляться слагаемые, которые не затухают с уменьшением шага, и такие проверки помогают их найти.

Объяснение уравнения теплопроводности

Как было получено уравнение теплопроводности? Известно, что в физике уравнения являются символьной записью результатов экспериментов. Это означает, что все уравнения должны иметь интуитивную интерпретацию, основанную на наблюдениях за окружающим миром. Процесс распространения тепла в некотором объекте можно описать простым принципом: изменение температуры в отдельно взятой точке объекта по времени попропорционально разности температуры в этой точке и средней температуры окружающих точек. Другими словами, температура в точке стремится к средней температуре окружающих точек. Математически это можно записать как

После перестановок формула принимает знакомый вид

В этой формуле шаг по времени и шаг по пространству включены в коэффициент $\alpha$. Условие устойчивости теперь можно перефразировать: абсолютное изменение температуры по времени в отдельно взятой точке не должно превышать абсолютной разности температуры в этой точке и средней температуры окружающих точек.

Определения

В предыдущем разделе мы познакомились с методами решения ДУЧП на примере уравнения теплопроводности. Здесь мы рассмотрим основные определения, классификацию уравнений, а также определим, какое место в этой классификации занимает расмотренное ранее уравнение.

Маршевой (эволюционной) задачей называется задача, в которой решение ищется в незамкнутой области. Для того чтобы область была незамкнута, достаточно, чтобы одна из переменных не была ограничена сверху или снизу. Такая переменная называется маршевой. В расмотренной ранее задаче с уравнением теплопроводности и начальными условиями маршевой переменной является время. Решение таких задач строится путем моделирования физического процесса от начального момента времени до некоторого конечного, в котором нам нужно узнать значение искомой функции.

Явным разностным уравнением является уравнение, в котором значение искомой функции при значении маршевой переменной $t + \Delta t$ явно выражается через значения этой функции при значении маршевой переменной $t$. В случае, когда время является маршевой переменной, это означает, что последующие во времени значения искомой функции опререляются через предыдущие. Иначе, уравнение является неявным.

Для явных уравнений на каждом шаге новое значение искомой функции вычисляется по явной формуле, а для неявных необходимо решить систему уравнений. Разностное уравнение теплопроводности является явным.

Начальными условиями называются дополнительные уравнения, которые включаются в решаемую задачу и которые задают значение искомой функции, которое соответствует начальному значению маршевой переменной. В случае времени это значение функции в начальный момент времени. Как правило, начальные условия — это формулы или константы, а не полноценные уравнения.

Граничными условиями называются дополнительные уравнения, которые включаются в решаемую задачу и которые задают значение искомой функции на границах области, в которой ищется решение. Граничные условия, как правило, записываются в виде уравнений. Если это уравнение содержит только искомую функцию, то это условие Дирихле. Если это уравнение содержит только производную функции, то это условие фон Неймана. Если же уравнение содержит и то, и другое, то это смешанное условие (или смешанная задача).

Используя эти определения, можно сказать, что задача, которую мы решили в предыдущем разделе, это маршевая задача с явным разностным уравнением теплопроводности и начальными условиями.

Уравнение переноса

Это уравнение описывает перемещение жидкости или газа, а также перенос его свойств (температуры, влажности, солености и т.п.) за счет этого перемещения.

Здесь $\rho$ — это плотность жидкости, а $\vec\upsilon$ — это вектор скорости жидкости. В такой записи это уравнение называется уравнением непрерывности. Оно показывает, что масса жидкости, которая покинула некоторый конечный объем, равна массе жидкости, которая прибыла в этот объем: закон сохранения массы для конечного объема. В одномерном случае уравнение принимает вид

Запишем разностное уравнение, используя разность вперед по времени и центральную разность по пространству.

Проверим уравнение на устойчивость с помощью метода фон Неймана.

Получившееся условие выполняется только в тривианльных случаях (когда скорость равна нулю): наше уравнение безусловно неустойчиво.

Проверим уравнение на сходимость с помощью рядов Тейлора. Раскладываем в ряд Тейлора исходную функцию в окрестности точки, соответствующей индексам $(i,j)$.

Подставляем получившиеся выражения в разностное уравнение.

Из получившихся результатов делаем вывод, что разностное уравнение сходится к дифференциальному, но оно безусловно неустойчиво.

Как же сделать его устойчивым? Заменим центральную разность на разность назад.

Проверим на устойчивость с помощью метода фон Неймана.

Это условие выполняется для положительной $\upsilon$. Если же скорость отрицательная, то для устойчивости необходимо использовать разность вперед по пространству.

Теперь проверим сходимость с помощью рядов Тейлора.

Делаем вывод, что разностное уравнение сходится к дифференциальному при уменьшении размеров шагов по времени и по пространству.

Итого получается следующее разностное уравнение.

Как было получено уравнение переноса? Перенос жидкости или какого-либо ее свойства можно описать так: изменение массы в некотором объеме равно количеству массы, пришедшей из соседних объемов или ушедшей в соседние объемы посредством напраленного движения жидкости. Математически это можно записать как

Здесь предполагается, что масса движется только в одну сторону, поэтому из одной соседней ячейки она выходит, а в другую наоборот входит.

🌊🌊🌊

Итого, мы узнали, что ДУЧП является обобщением ОДУ на многомерное пространство. ДУЧП решаются путем преобразования в разностную схему. Разностная схема должна сходиться к исходному уравнению, что можно проверить, разложив в ряд Тейлора значения искомой функции в разных точках и удостоверившись, что остаточные члены стремятся к нулю при стремлении к нулю размера сетки. Разностная схема должна быть устойчива, что можно проверить методом фон Неймана, удостоверившись, что амплитуда решения уменьшается со временем. Также разностные схемы являются интуитивной записью физических законов, в которых бесконечно малые величины заменены на конечные величины. Физическая интуиция также позволяет объяснить условия устойчивости разностной схемы законами сохранения, которые должны соблюдаться в природе.

Уравнение переноса и диффузии можно записать как одно уравнение, и в таком виде оно является левой частью уравнения Навье—Стокса, которое описывает движение жидкости.

Задания

Уравнение переноса1 балл

Решите одномерное уравнение переноса для следующих начальных и граничных условий.

Уравнение диффузии2 балла

Решите двухмерное (x и y) уравнение диффузии для следующих начальных и граничных условий.

Уравнение переноса-диффузии3 балла

Решите двухмерное (x и y) уравнение конвекции-диффузии (сумма уравнений переноса и диффузии) для следующих начальных и граничных условий.

Видео

2023

2022

Доска

2023

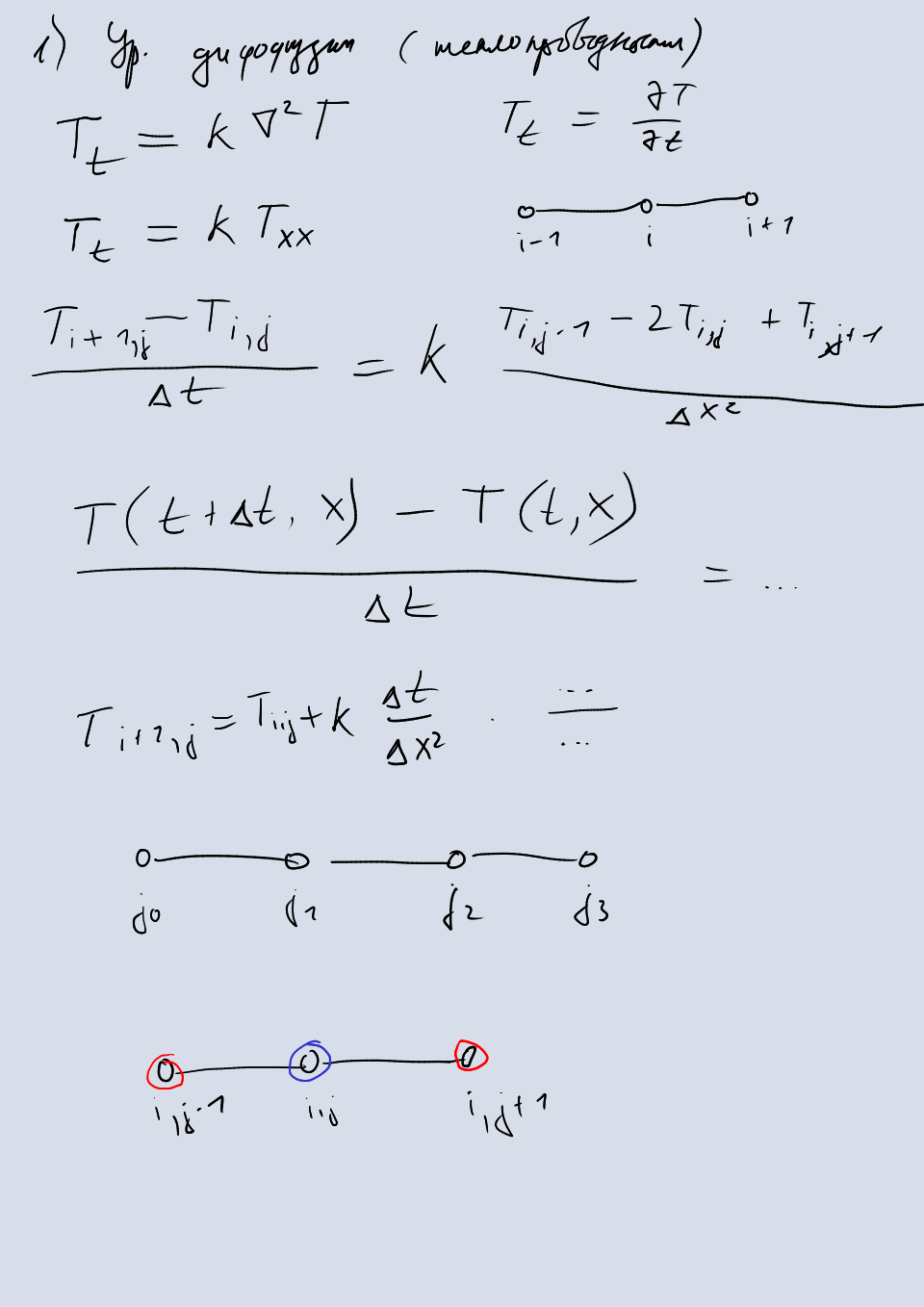
2022