§ 3. Локальная оптимизация

Математическая постановка задачи

Математическая оптимизация функций — это поиск экстремумов функции или значений аргументов функции, при котором она принимает максимальное/минимальное значение. С математической точки зрения, оптимизация — это определение значений аргументов, при которых производные функции принимают определенные занчения. Для того чтобы разобраться в терминологии, рассмотрим математическую постановку задачи оптимизации.

Критической точкой называется точка из области определения функции, в которой функция либо не имеет производную, либо эта производная равна нулю.

Точкой перегиба называется точка из области определения функции, в которой первая производная функции равна нулю и не меняет знак в этой точке.

Экстремумом функции называется точка из области определения функции, в которой первая производная функции равна нулю и меняет в этой точке знак на противоположный.

Минимумом функции называется точка из области определения функции, в которой первая производная функции равна нулю, отрицательна слева от этой точки и положительна справа от нее.

Максимумом функции называется точка из области определения функции, в которой первая производная функции равна нулю, положительна слева от этой точки и отрицательна справа от нее.

Также для определения минимума и максимума можно воспользоваться второй производной функции: если в точке из области определения функции первая производная равна нулю, а вторая производная больше нуля, то это точка минимума; если же вторая производная меньше нуля, то это точка максимума. Если вторая производная равна нулю в этой точке, то аналогичный анализ следует произвести с производными более высоких порядков.

Итак, что же нужно сделать, чтобы найти экстремум функции? Необходимо найти первую производную этой функции, приравнять ее нулю и из получившегося уравнения определить, чему равен аргумент этой функции:

$f(x) \rightarrow \text{max} \Rightarrow f'(x) = 0 \wedge f''(x) \lt 0, \\ f(x) \rightarrow \text{min} \Rightarrow f'(x) = 0 \wedge f''(x) \gt 0.$

Найдем точку минимума параболы:

$f(x) = x^2 \rightarrow \text{min}, \\ f'(x) = 2x = 0, \\ f''(x) = 2 \gt 0.$

Из получившихся уравнений очевидно, что функция имеет минимум в точке $x=0$.

Теперь найдем точку минимума одномерной функции Растригина, которая используется для проверки корректности работы методов оптимизации:

$f(x) = 10 + x^2 - 10 \cos(2\pi x)\rightarrow \text{min}, \\ f'(x) = 2x + 20\pi \sin(2 \pi x) = 0, \\ f''(x) = 2 + 40\pi^2 \cos(2 \pi x) \gt 0.$

Из получившихся уравнений не очевидно, какие точки являются экстремумами функции: можно лишь заметить, что точка $x=0$ удовлетворяет обоим уравнениям. Однако, если нарисовать график этой функции, станет понятно, что эта точка является глобальным минимумом, а помимо нее есть множество локальных минимумов и максимумов.

Функция называется выпуклой вниз (вверх), если отрезок между двумя любыми точками графика функции лежит не ниже (выше) графика. Парабола из первого примера является выпуклой вверх, а функция Растригина является невыпуклой. Для выпуклых функций локальный экстремум является также глобальным, а для невыпуклых функций это утверждение в общем случае неверно. Как следствие, для выпуклых и невыпуклых функций численные методы оптимизации кардинально различаются.

Теперь рассмотрим оптимизацию многомерных функций. Для них существуют смешанные производные, из-за чего данные ранее определения для них нужно модифицировать.

Экстремумом многомерной функции является точка из области определения функции, в которой градиент функции равен нулю, а гессиан (определитель матрицы Гессе) знакоопределен (принимает либо всегда положительные, либо всегда отрицательные значения).

Градиентом функции является вектор, каждая компонента которого является частной производной функции по соответствующей координате. Направление градиента совпадает с направление наибольшего роста функции, а длина равна скорости роста функции в этом направлении. Градиент это многомерный аналог производной, и эквивалентен производной в одномерном случае. Градиент двухмерной фукнции обозначается как $\nabla f(x,y) = \text{grad}\,f(x,y) = \left[\begin{array}{l}f'_x\\f'_y\end{array}\right].$

Матрицей Гессе функции является матрица Якоби для частных производных этой функции по каждой из координат. Матрица Гессе двухмерной функции обозначается как $\mathbb{H}\,f(x,y) = \left[\begin{array}{ll} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \\ \end{array}\right],$ где нижними индексами обозначаются производные по соответствующим координатам. Если смешанные производные непрерывны, то порядок взятия производных неважен, и матрица является симметричной. Матрица Гессе не является многомерным аналогом производных второго порядка, а является самостоятельным понятием.

Матрицей Якоби для системы уравнений

называется матрица вида

Гессианом называется определитель матрицы Гессе. Для двухмерного случая определитель равен

Теперь найдем точку минимума двухмерной функции Розенброка:

Таким образом, функция Розенброка имеет минимум в точке $x=1,y=1$.

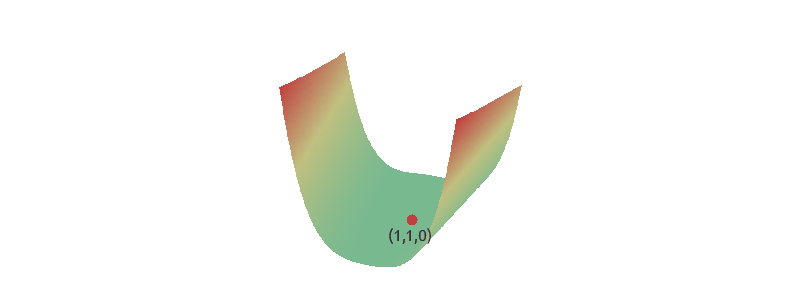
Итого, мы узнали, что математическая оптимизация функций заключается в поиске точек минимумов и максимумов этой функции. В одномерном случае в этих точках несколько первых производных (но не меньше одной) равны нулю, а знак следующей за ними производной отличен от нуля и показывает, является ли эта точка минимумом или максимумом. Для многомерных функций понятие производных первого порядка обобщается понятием градиента, а тип экстремума определяется знаком Гессиана. Аналитическая оптимизация функций возможна только при условии существования всех производных, присутствующих в формулах. Функции делятся на выпуклые, у которых глобальная точка минимума (максимума) совпадает с локальной точкой минимума (максимума), и невыпуклые, для которых это утверждение в общем случае не выполняется. Аналитическая оптимизация одинакова для всех функций, однако численные методы сильно отличается.

Методы поиска локальных экстремумов

Методы оптимизации, как правило, включают в себя следующие основные компоненты:

• подобласть определения функции, внутри которой ищется точка экстремума;
• целевую функцию, которая обращается в ноль в точке экстремума;
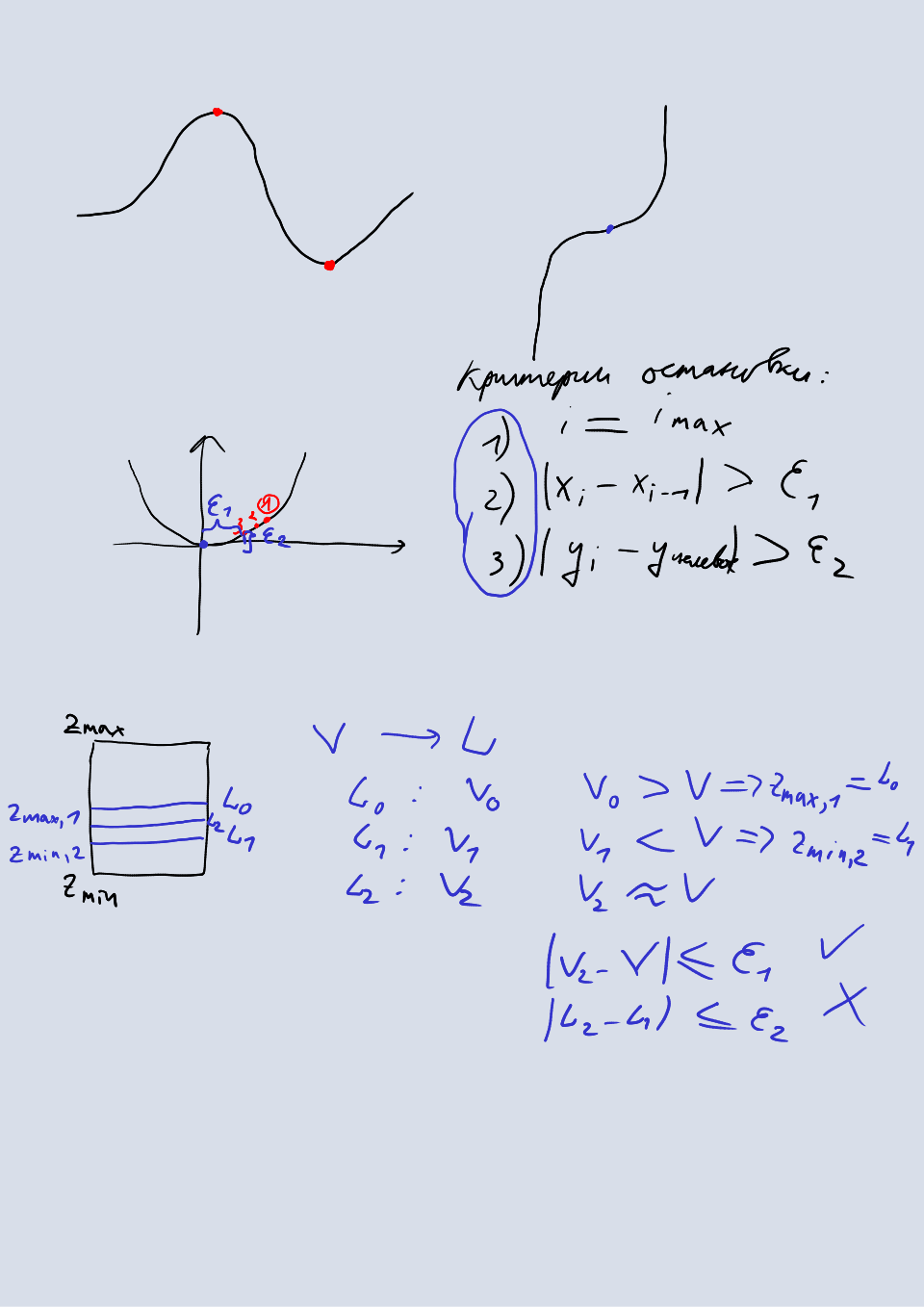
• критерии остановки итераций; как правило, это достижение нужной точности аргумента и значения целевой функции, а также достижения максимально допустимого числа итераций или максимального количества раз, которое вычисляется значение целевой функции.

Метод полного перебора

Наиболее простым методом оптимизации является полный перебор. Суть метода заключается в разбиении области определения оптимизируемой функции на равные промежутки (подобласти) и вычислении целевой функции в каждой точке получившейся сетки. Из получившихся значений выбирается минимальное. Если выбрать размер промежутка равный допустимой погрешности аргумента, тогда погрешность аргумента также будет в пределах допустимой (при этом погрешность функции может быть иной).

Этот метод является самым ресурсоемким из существующих, однако он работает для любых функций: дискретно заданных и непрерывных, с производными и без. Также этот метод легко ускорить на многопроцессорной машине или кластере таких машин, запустив поиск параллельно в нескольких потоках. Его применяют в задачах оптимизации, имеющих нефизическую природу (машинное обучение), а также в задачах, в которых стохастические методы неприемлемы. Без большого кластера этот метод в реальных задачах применяться не может.

Метод бисекции

Для выпуклых функций наиболее простым методом оптимизации является метод бисекции (или метод половинного деления). Этот метод основан на следующем наблюдении: если на концах некоторого промежутка целевая функция принимает значения различных знаков, значит на этом промежутке находится точка, в которой она обращается в ноль (точка экстремума исходной функции). Как только мы находим такой промежуток, мы делим его пополам и в качестве нового промежутка выбираем ту его часть, на концах которой целевая функция принимает значения различных знаков. Преимуществами данного метода является простота и отсутствие требования существования производной. Метод бисекции обобщается на многомерный случай тривиальным образом: вместо промежутка для одной координаты мы на каждой итерации повторяем все действия для каждой из координат.

Применим метод бисекции к задаче затопления отсеков морского объекта жидкостью. Мы будем определять уровень жидкости по известному объему и геометрии отсека. В данном случае целевая функция запишется как

Здесь $h$ — искомый уровень жидкости, значения которого подбирает метод оптимизации, $V_0$ — известный объем жидкости в отсеке, $g$ — функция, которая вычисляет объем жидкости по заданному уровню $h$. В качестве подобласти определения функции возьмем промежуток от нуля до максимального уровня жидкости в отсеке $h_\text{max}$. Наконец, в качестве критерия остановки выберем достижение нужной точности аргумента и значения целевой функции $\left|f(h)\right| < \epsilon_f \wedge \left|h-h_0\right| < \epsilon_a,$ где $\epsilon_f$ — допустимая погрешность функции, $\epsilon_a$ — допустимая погрешность аргумента, $h_0$ — значение аргумента на предыдущей итерации. В данной задаче эти погрешности имеют физические величины (метры и кубометры), что удобно при задании их значений.

В этой задаче целевая функция является производной, которая равна нулю в точке экстремума, а исходной функции, экстремум которой мы ищем, в этой задаче нет. По сути, мы ищем корень в общем случае нелинейного уравнения $f(h) = 0$, а это значит, что метод бисекции, как и остальные методы оптимизации, можно использовать для нахождения корней уравнений.

В методе бисекции выбор точки, которая разделяет промежуток на две части, произволен. Это сделало возможным модификации данного метода, которые используют золотое сечение и числа Фибоначчи для выбора точки разделения. Скорость сходимости метода бисекции и его модификаций линейна: погрешность аргумента уменьшается на каждой итерации вдвое, то есть линейно зависит от количества итераций. Целевая функция метода бисекции должна быть монотоной, то есть не убывать (не возрастать) на любой подобласти из области определения функции.

Для того чтобы повысить скорость сходимости, используют дополнительную информацию о функции — ее производную. Среди методов, которые используют эту информацию, наиболее распространенными являются метод Ньютона и метод градиентного спуска.

Метод Ньютона

Метод Ньютона использует производные первого и второго порядка, для того чтобы сделать сходимость квадратичной. Поскольку метод численный, нам необходимо некоторое универсальное представление оптимизируемой функции, которое использует производные. В методе Ньютона в качестве такого представления используется разложение в ряд Тейлора в окрестности точки, которая является приближением к точке экстремума:

Здесь $a$ — точка, в окрестности которой производится разложение, $f$ — оптимизируемая функция, а $f^{(n)}$ — производная порядка $n$. Теперь разложим функцию $f$ в окрестности точки $x_0$ в ряд Тейлора и положим $x=x_0+\epsilon$. Возьмем из получившегося ряда первые три слагаемых:

Возьмем производную по $\epsilon$ от получившегося выражения и получим

В точке экстремума получившееся выражение принимает значение равное нулю, откуда получаем, что

Отсюда можно получить следующее приближение точки экстремума как

Это уравнение вычисляется на каждой итерации метода Ньютона для уточнения решения.

Метод Ньютона также можно использовать для решения нелинейных уравнений. Для этого нет необходимости брать производную, поскольку мы ищем корень уравнения $f(x) = 0$, а также мы возьмем только первые два слагаемых из ряда Тейлора. В итоге на каждой итерации новое приближение будет вычисляться по формуле

Преимуществом метода Ньютона по сравнению с методом бисекции является квадратичная сходимость, что является следствием использования первых двух слагаемых в ряде Тейлора (в случае взятия производной порядок третьего слагаемого уменьшается, поэтому сходимость все равно квадратичная). Скорость сходимости можно повысить, взяв больше слагаемых из ряда, но тогда придется вычислить производные более высоких порядков.

Недостатоком метода Ньютона является использование производных, то есть метод нельзя применить к функциям, производные которых не существуют. Если функция задана дискретно, то для определения производных применяются разностные схемы или другие методы, которые будут обсуждаться в последующих разделах. Это может сильно замедлить программную реализацию метода, особенно в многомерных случаях.

В многомерном случае производная первого порядка заменяется градиентом, а производная второго порядка матрицей Гессе. Матрицу, обратив, можно переместить в числитель. Тогда получится

Обратная матрица Гессе находится либо с помощью методов обращения матриц, либо путем решения системы линейных уравнений $\mathbb{H}f(\vec{x}_n) \vec{h} = \nabla f(\vec{x}_n),$ где $\vec{h} = \mathbb{H}^{-1}f(\vec{x}_n) \, \nabla f(\vec{x}_n),$ относительно $\vec{h}$. Методы решения систем линейных уравнений и методы обращения матриц будут рассмотрены в последующих разделах.

Метод градиентного спуска

Метод градиентного спуска является альтернативой методу Ньютона, в котором не используются производные второго порядка, а значит нет необходимости вычислять матрицу Гессе. Идея метода заключается в том, что направление градиента совпадает с направлением наискорейшего роста функции, а значит, если двигаться в этом (обратном) направлении, то мы достигнем максимума (минимума). Другое название метода — метод наискорейшего спуска. Каждое новое приближение точки минимума вычисляется по формуле

Здесь $\epsilon_n$ является шагом спуска — некоторым небольшим числом, которое регулирует скорость спуска: если взять слишком большое число, то метод разойдется; если взять слишком маленькое число, то метод сильно замедлится. Для определения оптимального шага существует несколько методов:

• использовать матрицу Гессе по аналогии с методом Ньютона;
• линейный поиск в направлении градиента: увеличивать шаг до тех пор, пока функция убывает, не изменяя при этом градиент.

Метод градиентного спуска в отличие от метода Ньютона имеет линейную сходимость.

Задания

Одномерная оптимизация1 балл

• Реализуйте одномерный метод бисекции и проверьте его на функции Растригина.
• Реализуйте одномерный метод Ньютона и проверьте его на функции Растригина.
• Сравните скорость сходимости двух методов.

Многомерная оптимизация2 балла

• Реализуйте двухмерный метод бисекции и проверьте его на функции Растригина.
• Реализуйте двухмерный метод Ньютона и проверьте его на функции Растригина.
• Сравните скорость сходимости двух методов.

Затопление отсеков2 балла

С помощью метода бисекции реализуйте две функции:

• определение уровня жидкости в отсеке по известному объему,
• определение объема жидкости в отсеке по известному уровню.

Геометрия отсека задается массивом треугольных граней в формате STL (файл tank.stl). Для вычисления объема отсеченной горизонтальной поверхностью жидкости части отсека используйте формулу знакопеременного объема тетраэдра

Для этого расположите вершину $\vec{d}$ тетраэдра в произвольной точке на поверхности жидкости, а за основание примите треугольную грань отсека. Просуммировав знакопеременные объемы для каждой грани, находящейся ниже плоскости отсечения, вы получите объем заполненной жидкостью части отсека.

При отсечении учитывайте грани, хотя бы одна вершина которых находится ниже плоскости отсечения. Дополнительно разбивать грани плоскостью в этом задании не требуется.

Затопление отсеков v21 балл

В дополнение к предыдущему заданию разбейте грани отсека, сквозь которые прошла плоскость поверхности жидкости, на треугольники меньшего размера и вычислите объем, используя эти треугольники. Сравните точность этого способа и предыдущего (без разбиения).

Видео

2023

2022

Доска

2023