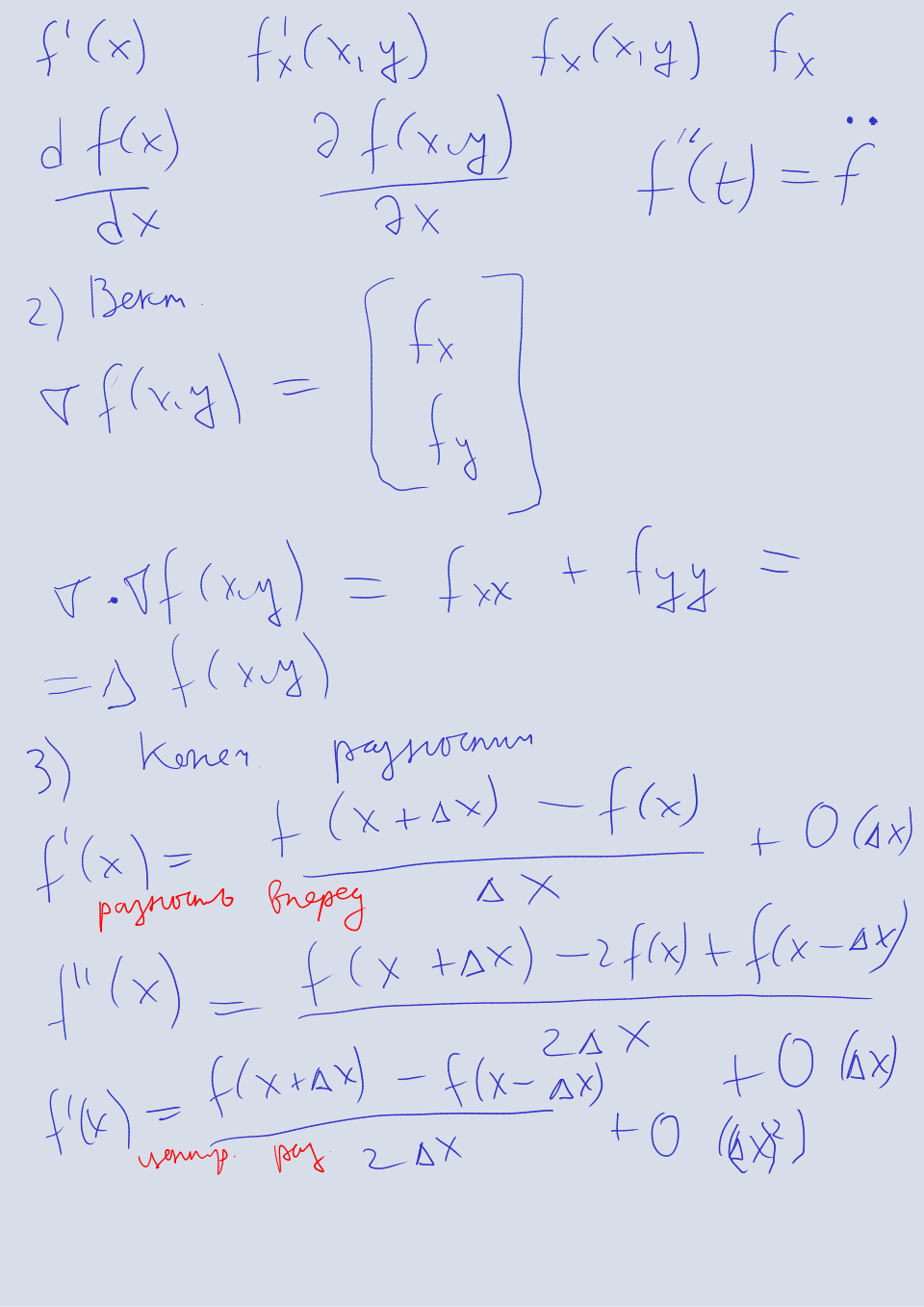§ 9. Численное дифференцирование

Математическая постановка задачи

Перед тем как преходить к обсуждению численных методов взятия производной, мы кратко обсудим необходимые чисто математические определения и обозначения.

Математически производная функции $f$ определяется как

Геометрическая интерпретация производной — это тангенс угла наклона касательной к графику функции в точке $x$. Непрерывность функции является необходимым, но недостаточным условием существования производной.

Для производной используют разные обозначения.

• Наиболее распространено обозначение Лейбница через дифферециалы $\frac{df(x)}{dx} = f'(x).$
• Для производных по времени используется обозначение Ньютона $\dot{f}(t) = f'(t)$.
• В математической физике распространено обозначение с помощью индексов (по аналогии с тензорами) $f_x(x) = f'(x)$, которое является самым кратким для частных производных. В последующих разделах мы будем использовать только это обозначение.

Помимо обычных производных существуют частные производные — производные функции по одному аргументу. Для функций одного аргумента частная и обычная производные совпадают. Для функции двух аргументов частные производные определяются как

Наконец, существуют смешанные производные — это производные от нескольких аргументов сразу

Для функции, у которой существуют производные $f_x,f_y,f_{xy},f_{yx}$, частные производные равны между собой: $f_{xy}=f_{yx}$. В общем случае это не так.

В многомерном случае для обозначения производной используют оператор набла

Оператором называют некоторую функцию, которая обычно записывается с помощью математических символов. Такая запись позволяет производить операции над этими символами, вместо того чтобы производить операции над результатом этой функции. Оператор набла принимает на вход функцию, а возвращает вектор ее частных производных. Сумма вторых производных обозначается как

$\nabla^2 f(x,y) = \nabla\cdot\nabla f(x,y) = \frac{\partial^2}{\partial^2 x}f(x,y)+\frac{\partial^2}{\partial^2 y}f(x,y).$

Здесь точкой обозначается скалярное произведение векторов. Вторую производную можно записать и в векторном виде, однако такая запись редка, и отдельного символа для нее нет:

$\nabla\circ\nabla f(x,y) = \left[\begin{array}{l}\frac{\partial^2}{\partial^2 x}f(x,y)\\\frac{\partial^2}{\partial^2 y}f(x,y)\end{array}\right].$

Здесь кругом обозначается покомпонентное произведение векторов (произведение Адамара).

Итого, производная показывает приращение функции относительно приращения аргумента в каждой точке области определения функции. Понятие производной обобщается на многомерное пространство, в котором приращение функции определяется относительно отдельно взятой оси этого пространства. Теперь рассмотрим различные численные методы аппроксимации производных.

Конечные разности

Очевидно, взяв формулу производной из определения и некоторый малый шаг $\Delta x$, можно получить простейшую аппроксимацию

Эта формула называется разностью вперед. Также существует разность назад

которая отличается лишь направлением шага, и центральная разность

Все эти разности при $\Delta x \rightarrow 0$ дают точное определение производной. Конечные разности интуитивны, однако их обобщение для аппроксимаций более высокой точности неочевидно, и может происходить несколькими способами. Сейчас мы рассмотрим эти способы.

Аппроксимация с помощью ряда Тейлора

Ряд Тейлора ставит в соответствие значению функции в определенной точке линейную комбинацию значений ее производных. Наша идея состоит в том, чтобы разложить функцию в ряд Тейлора в нескольких точках, отличающихся на $\Delta x$, и из получивишхся уравнений получить выражение для производной.

Для удобства будем использовать альтернативную запись этого ряда для $x + \Delta x$

Теперь разложим функцию в точках $x + \Delta x$ и $x - \Delta x$ до второго слагаемого и получим

Вычитаем из первого уравнения второе и получаем формулу для центральной разности

Аналогично можно получить формулы для других разностей, рассмотренных ранее. Более точные формулы получаются, если разложить функцию в трех и более точках.

Здесь мы воспользовались символом о большое, для того чтобы показать асимптотическую точность наших аппроксимаций. Этот символ используют при разложении в ряд с конечным набором слагаемых. Этот символ означает, что сумма оставшихся слагаемых по абсолютной величине не превышает выражение внутри скобок, домноженное на некоторую константу. Центральные разности имеют точность второго порядка, а разность вперед и назад первого.

Полиномиальная аппроксимация

Более автоматизированным способом аппроксимации производных является представление функции в виде полинома. Мы записываем значение функции в точках $x, x + \Delta x, \ldots$ с помощью полинома, решаем получившуюся систему уравнений, чтобы узнать коэффициенты полинома, а затем получаем формулы для производных путем дифференцирования полинома.

Запишем систему уравнений для функции в двух точках

Решая эту систему, получим

Первая производная от полинома равна $a_2$, поэтому это и есть наш финальный ответ:

Полиномы более высоких порядков дадут более точные аппроксимации производных. В общем случае аппроксимация с помощью ряда Тейлора и полиномиальная аппроксимация дают разные формулы, это только для простых случаев формулы одинаковы. Полиномиальная аппроксимация удобна для автоматизированного создания формул конечных разностей с помощью символьных вычислений. Формулы для последнего примера были получены в программе Mathics с помощью следующего кода.

Solve[{a1 + a2 x == f[x],a1 + a2 (x+dx) == f[x+dx]}, {a1,a2}] // TeXForm

Этот код без изменений работает в программе Mathematica. Аналогичный код можно написать и для Matlab. При должном усердии можно написать генератор формул конечных разностей для полиномов произвольных порядков.

Аппроксимация с помощью преобразования Фурье

Это самый необычный и редко используемый способ нахождения производной. Идея заключается в том, чтобы использовать свойство преобразования Фурье, которое связывает преобразование Фурье исходной функции и ее производной, а затем вычислить значение производной, взяв обратное преобразование от обоих частей уравнения.

На первый взгляд формула кажется сложной и неэффективной. Так и есть в случае единичного взятия производной, однако в решении уравнений в частных производных можно заранее применить преобразование Фурье к обоим частям решаемого уравнения, затем решить уравнение некоторым способом, а в конце взять обратное преобразование Фурье от обоих частей решения. Такой способ решения уравнений в частных производных может оказаться более эффективным, чем способы, основанные на других аппроксимациях производных.

Производная по направлению

Производная по направлению — это обобщение формулы производной для разниц, взятых не вдоль конкретной оси координат, а вдоль произвольной оси. Производная вдоль оси координат является частным случаем производной по направлению. Производная по направлению записывается как

🌊🌊🌊

Мы узнали, что производные можно аппроксимировать различными способами и с различной точностью. Теперь мы рассмотрим задачи, в которых применяются эти аппроксимации, а именно дифференциальные уравнения в частных производных (ДУЧП).

Задания

Уравнение второго порядка v21 балл

Решите явным методом уравнение второго порядка, используя центральную разность для представления второй производной. Подберите шаг, при котором решение не расходится. Уравнение имеет вид

Значение функции $f$ и ее первой производной при $t=0$ произвольное.

Затопление отсеков v32 балла

Решите задачу затопления отсеков с помощью метода Ньютона. Для вычисления первой и второй производной воспользуйтесь центральными разностями. Величину шага по $z$ выберите самостоятельно.

Производная по направлению3 балла

Перед вами цилиндр, который разбит на тетраэдры. Напишите программу, которая моделирует распространение тепла внутри цилиндра. Температура определена в центре каждого тетраэдра, начальное распределение — нормальное с максимумом в центре цилиндра. Соседние тетраэдры обмениваются теплом по слеующему закону: изменение температуры тетраэдра за один шаг по времени равно среднему арифметическому производных температуры по направлению к центру соседних тетраэдров. Другими словами, изменение равно среднему арифметическому разности температур текущего с каждым из соседних тетраэдров, нормированной на расстояние до центров этих соседних тетраэдров.

Здесь $n$ — количество соседних тетраэдров, $T_{i,j}$ — температура тетраэдра $j$ в момент времени $i$, $T_{i}$ — температура текущего тетраэдра в момент времени $i$, $\vec{x}$ — координата центра тетраэдра, $\alpha$ — коэффициент теплопроводности.

Для выполнения этого задания вам понадобится таблица смежности тетраэдров. Тетраэдры являются смежными, если три любых вершины одного тетраэдра совпадают с тремя любыми вершинами другого.

Видео

2023

2022

Доска

2023

2022